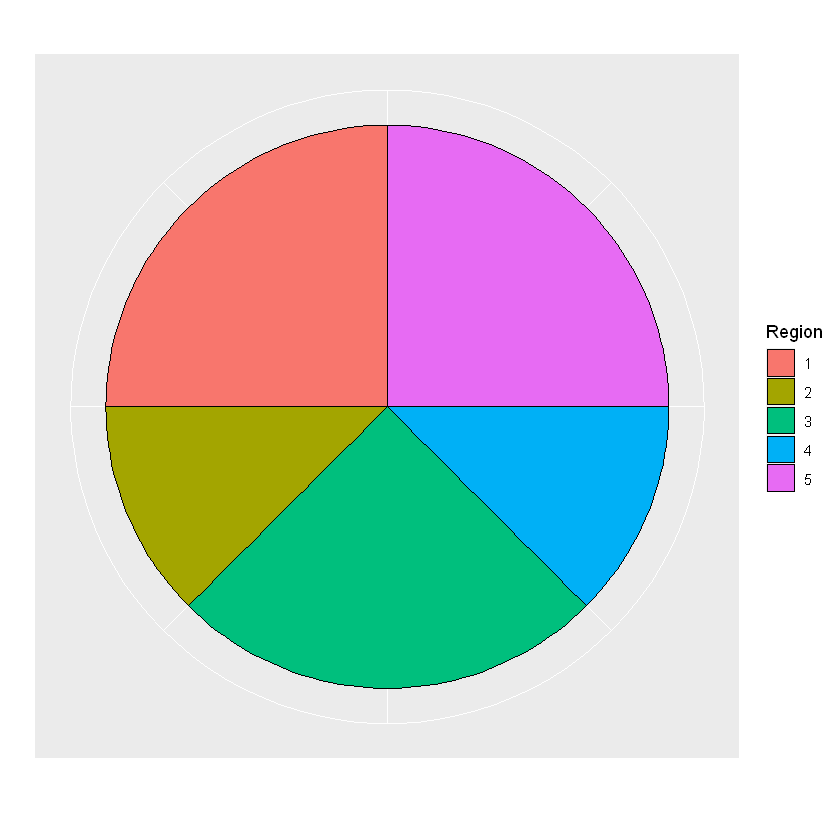1
2
3
4
5
6
7
8
| # funzioni
# https://mran.microsoft.com/snapshot/2017-12-11/web/packages/TeachBayes/TeachBayes.pdf
source("https://raw.githubusercontent.com/AlbGri/AlbGri.github.io/master/assets/files/R/LearningBayes.R")
# lib
suppressMessages(library(ggplot2))
suppressMessages(library(gridExtra))
suppressMessages(library(dplyr))
|
Introduction
Probabilità
1
2
| areas <- c(2, 1, 2, 1, 2)
spinner_plot(areas)
|
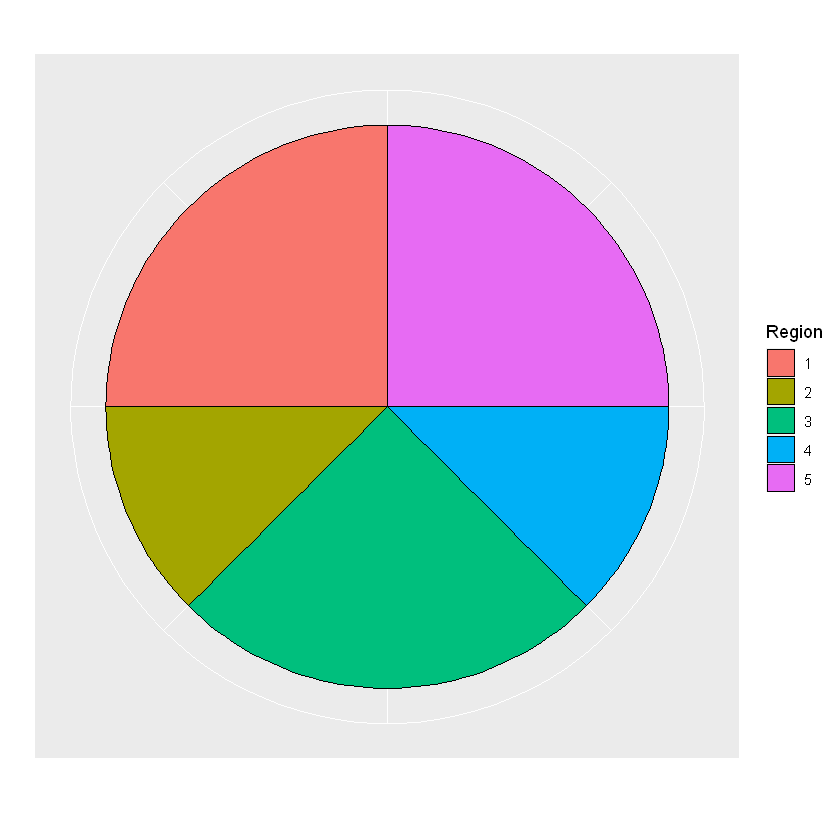
1
2
3
4
| # distribuzione di probabilità
df <- data.frame(Region = 1:5, areas,
Probability = areas / sum(areas))
df
|
A data.frame: 5 × 3
| Region | areas | Probability |
|---|
| <int> | <dbl> | <dbl> |
|---|
| 1 | 2 | 0.250 |
| 2 | 1 | 0.125 |
| 3 | 2 | 0.250 |
| 4 | 1 | 0.125 |
| 5 | 2 | 0.250 |
Stima classica
\[P(\mbox{dispari})=0.25+0.25+0.25=0.75\]
1
| df %>% filter(Region %in% c(1,3,5))
|
A data.frame: 3 × 3
| Region | areas | Probability |
|---|
| <int> | <dbl> | <dbl> |
|---|
| 1 | 2 | 0.25 |
| 3 | 2 | 0.25 |
| 5 | 2 | 0.25 |
\[P(\mbox{Maggiore di 3})=0.125+0.25=0.375\]
1
| df %>% filter(Region > 3)
|
A data.frame: 2 × 3
| Region | areas | Probability |
|---|
| <int> | <dbl> | <dbl> |
|---|
| 4 | 1 | 0.125 |
| 5 | 2 | 0.250 |
Stima con simulazione
1
2
3
| # genero un campione casuale di 10 osservazioni delle 5 regioni con le rispettive probabilità di estrazione
ten_spins <- spinner_data(areas, 10)
ten_spins
|
1 5 5 5 2 1 1 3 3 4
1
2
3
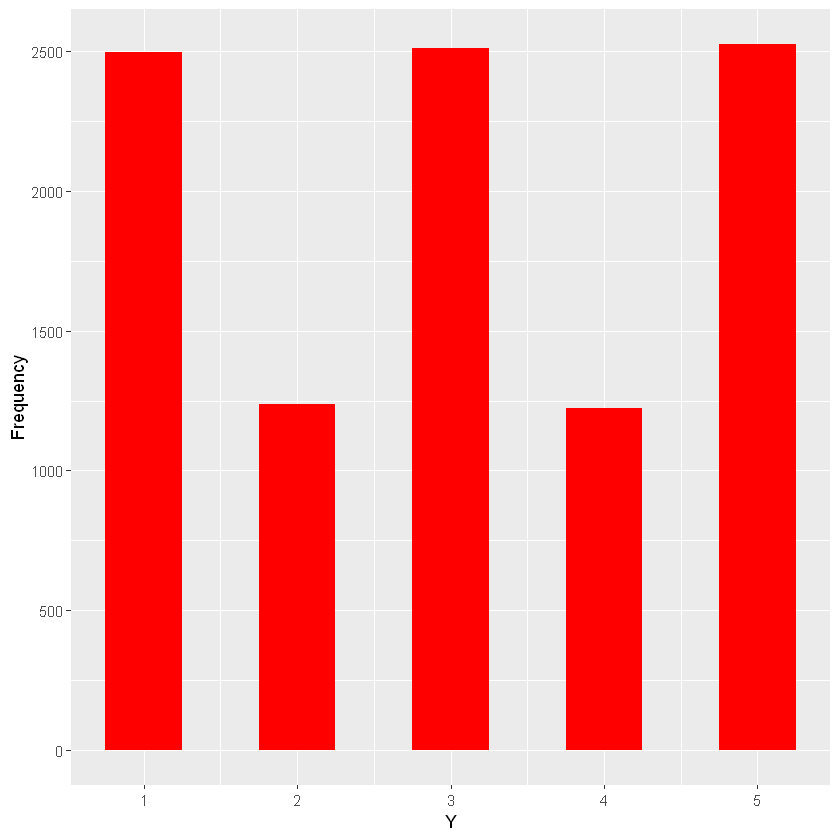
| # genero un campione casuale di 10000 osservazioni delle 5 regioni con le rispettive probabilità di estrazione
many_spins <- spinner_data(areas, 10000)
bar_plot(many_spins)
|
1
2
3
4
5
| # distribuzione di frequenza
S <- data.frame(Region = many_spins) %>%
group_by(Region) %>%
summarise(N=n(), .groups = 'drop_last')
S
|
A tibble: 5 × 2
| Region | N |
|---|
| <int> | <int> |
|---|
| 1 | 2499 |
| 2 | 1238 |
| 3 | 2512 |
| 4 | 1224 |
| 5 | 2527 |
\[P(\mbox{Region}=1)\]
1
| S %>% filter(Region==1) %>% sum() / 1000
|
2.5
Bayes’ rule
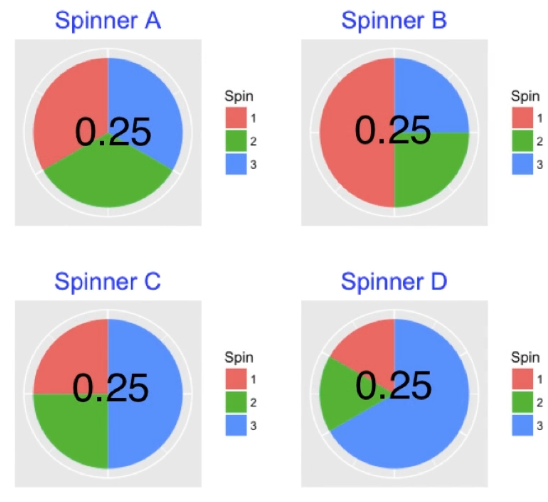
Si hanno 4 spinner, ciascuno diviso in 3 colori (Rosso, Verde e Blu).
Obiettivo: se so che è uscito Rosso, quale spinner mi aspetto sia stato utilizzato?
1
2
| bayes_df <- data.frame(Model = paste("Spinner", c("A", "B", "C", "D")))
bayes_df
|
A data.frame: 4 × 1
| Model |
|---|
| <chr> |
|---|
| Spinner A |
| Spinner B |
| Spinner C |
| Spinner D |
Distribuzione a priori
Non sapendo se alcuni di questi spinner vengono scelti più o meno facilmente, assegno equiprobabilità per la scelta dello spinner.
1
2
3
| # distribuzione a priori
bayes_df$Prior <- rep(0.25, 4)
bayes_df
|
A data.frame: 4 × 2
| Model | Prior |
|---|
| <chr> | <dbl> |
|---|
| Spinner A | 0.25 |
| Spinner B | 0.25 |
| Spinner C | 0.25 |
| Spinner D | 0.25 |
Verosimiglianza
Conosciamo la probabilità di estrazione del colore Rosso per ciascun spinner
1
2
3
| # probabilità di ottenere rosso
bayes_df$Likelihood <- round(c(1/3, 1/2, 1/4, 1/6), 2)
bayes_df
|
A data.frame: 4 × 3
| Model | Prior | Likelihood |
|---|
| <chr> | <dbl> | <dbl> |
|---|
| Spinner A | 0.25 | 0.33 |
| Spinner B | 0.25 | 0.50 |
| Spinner C | 0.25 | 0.25 |
| Spinner D | 0.25 | 0.17 |
Distribuzione a posteriori
“Turn the Bayesian Crank” significa calcolare le probabilità a posteriori usando la regola di Bayes
1
2
3
| # ne fa il prodotto e normalizza rispetto la somma
bayes_df <- bayesian_crank(bayes_df)
bayes_df
|
A data.frame: 4 × 5
| Model | Prior | Likelihood | Product | Posterior |
|---|
| <chr> | <dbl> | <dbl> | <dbl> | <dbl> |
|---|
| Spinner A | 0.25 | 0.33 | 0.0825 | 0.264 |
| Spinner B | 0.25 | 0.50 | 0.1250 | 0.400 |
| Spinner C | 0.25 | 0.25 | 0.0625 | 0.200 |
| Spinner D | 0.25 | 0.17 | 0.0425 | 0.136 |

Quindi, mi aspetto che lo spinner \(B\) sia stato quello utilizzato (in quanto l’a priori, aggiornata con la verosimiglianza, cioè l’a posteriori, fa emergere che lo spinner \(B\) sia il più probabile).
1
2
| # confronto distribuzioni
prior_post_plot(bayes_df)
|

Sequential Bayes
Se si continua, l’a posteriori sarà la nuova distribuzione a priori.
Cosa accade se ora se si estrae il blu?
1
2
3
| # nuova priori
bayes_df2 <- bayes_df %>% select(Model, Posterior) %>% rename(Prior=Posterior)
bayes_df2
|
A data.frame: 4 × 2
| Model | Prior |
|---|
| <chr> | <dbl> |
|---|
| Spinner A | 0.264 |
| Spinner B | 0.400 |
| Spinner C | 0.200 |
| Spinner D | 0.136 |
1
2
3
| # verosimiglianza del blu
bayes_df2$Likelihood <- round(c(1/3, 1/4, 1/2, 2/3), 2)
bayes_df2
|
A data.frame: 4 × 3
| Model | Prior | Likelihood |
|---|
| <chr> | <dbl> | <dbl> |
|---|
| Spinner A | 0.264 | 0.33 |
| Spinner B | 0.400 | 0.25 |
| Spinner C | 0.200 | 0.50 |
| Spinner D | 0.136 | 0.67 |
1
2
3
| # posteriori: bayesian crank
bayes_df2 <- bayesian_crank(bayes_df2)
bayes_df2
|
A data.frame: 4 × 5
| Model | Prior | Likelihood | Product | Posterior |
|---|
| <chr> | <dbl> | <dbl> | <dbl> | <dbl> |
|---|
| Spinner A | 0.264 | 0.33 | 0.08712 | 0.2303299 |
| Spinner B | 0.400 | 0.25 | 0.10000 | 0.2643824 |
| Spinner C | 0.200 | 0.50 | 0.10000 | 0.2643824 |
| Spinner D | 0.136 | 0.67 | 0.09112 | 0.2409052 |
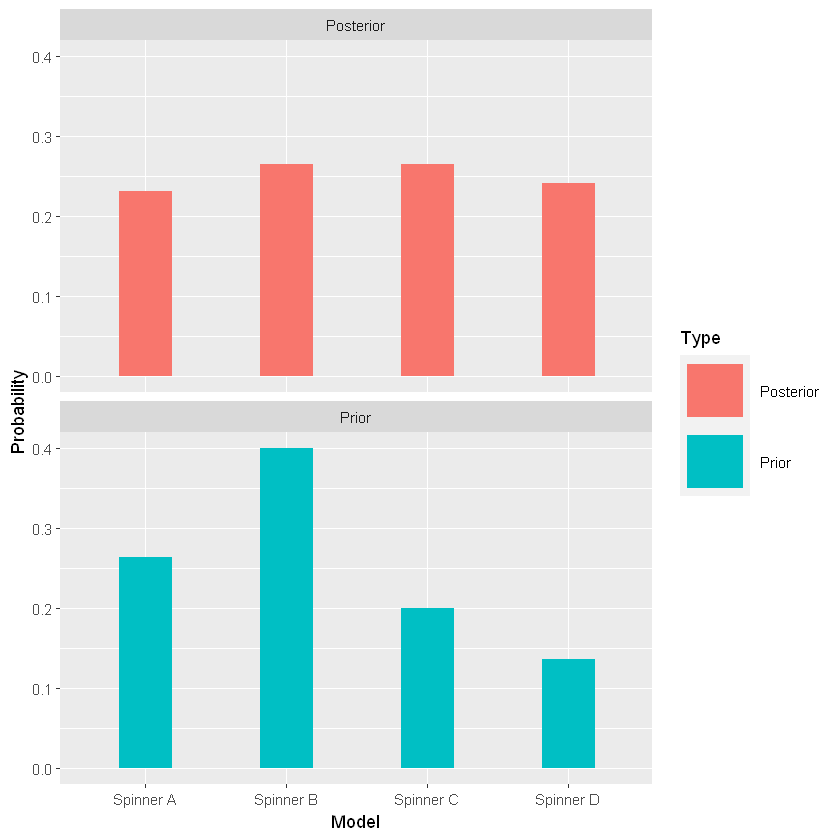
Ora lo spinner che più probabilmente è stato usato non è solo il \(B\) ma anche il \(C\)
1
2
| # confronto distribuzioni
prior_post_plot(bayes_df2)
|
1
2
| # clear environment
rm(list=ls())
|
Distribuzione a priori discreta
Distribuzione a priori (proporzione)
Sia \(p\) la proporzione di individui positivi
\(p \in \left\{0.3,0.4,...,0.8\right\}\)
La nostra sensibilità e/o conoscenza di dominio ci porta ad affermare che \(0.5\) (stessa numerosità di positivi e negativi) e \(0.6\) sono le proporzioni più plausibili per questo studio, due volte più probabili rispetto gli altri.
1
2
3
4
| bayes_df <- data.frame(P = seq(0.3,0.8,by=0.1),
Weight = c(1,1,2,2,1,1),
Prior = c(1,1,2,2,1,1)/8)
bayes_df
|
A data.frame: 6 × 3
| P | Weight | Prior |
|---|
| <dbl> | <dbl> | <dbl> |
|---|
| 0.3 | 1 | 0.125 |
| 0.4 | 1 | 0.125 |
| 0.5 | 2 | 0.250 |
| 0.6 | 2 | 0.250 |
| 0.7 | 1 | 0.125 |
| 0.8 | 1 | 0.125 |
Verosimiglianza (Binomiale)
A seguito della raccolta empirica dei dati da un campione, si ottengono 12 positivi su 20.
L’esperimento è binomiale: la probabilità di 12 successi su 20, con probabilità di successo \(p\)
\(L={20\choose 12}p^{12}(1-p)^{8}\)
1
2
3
4
5
| # verosimiglianza
bayes_df <- bayes_df %>%
mutate(Likelihood = round(dbinom(12, size=20, prob=bayes_df$P),3)) %>%
select(P, Prior, Likelihood)
bayes_df
|
A data.frame: 6 × 3
| P | Prior | Likelihood |
|---|
| <dbl> | <dbl> | <dbl> |
|---|
| 0.3 | 0.125 | 0.004 |
| 0.4 | 0.125 | 0.035 |
| 0.5 | 0.250 | 0.120 |
| 0.6 | 0.250 | 0.180 |
| 0.7 | 0.125 | 0.114 |
| 0.8 | 0.125 | 0.022 |
Distribuzione a posteriori
1
2
3
| # crank!
bayes_df <- bayesian_crank(bayes_df)
bayes_df
|
A data.frame: 6 × 5
| P | Prior | Likelihood | Product | Posterior |
|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
|---|
| 0.3 | 0.125 | 0.004 | 0.000500 | 0.00516129 |
| 0.4 | 0.125 | 0.035 | 0.004375 | 0.04516129 |
| 0.5 | 0.250 | 0.120 | 0.030000 | 0.30967742 |
| 0.6 | 0.250 | 0.180 | 0.045000 | 0.46451613 |
| 0.7 | 0.125 | 0.114 | 0.014250 | 0.14709677 |
| 0.8 | 0.125 | 0.022 | 0.002750 | 0.02838710 |
1
2
| # confronto
prior_post_plot(bayes_df)
|
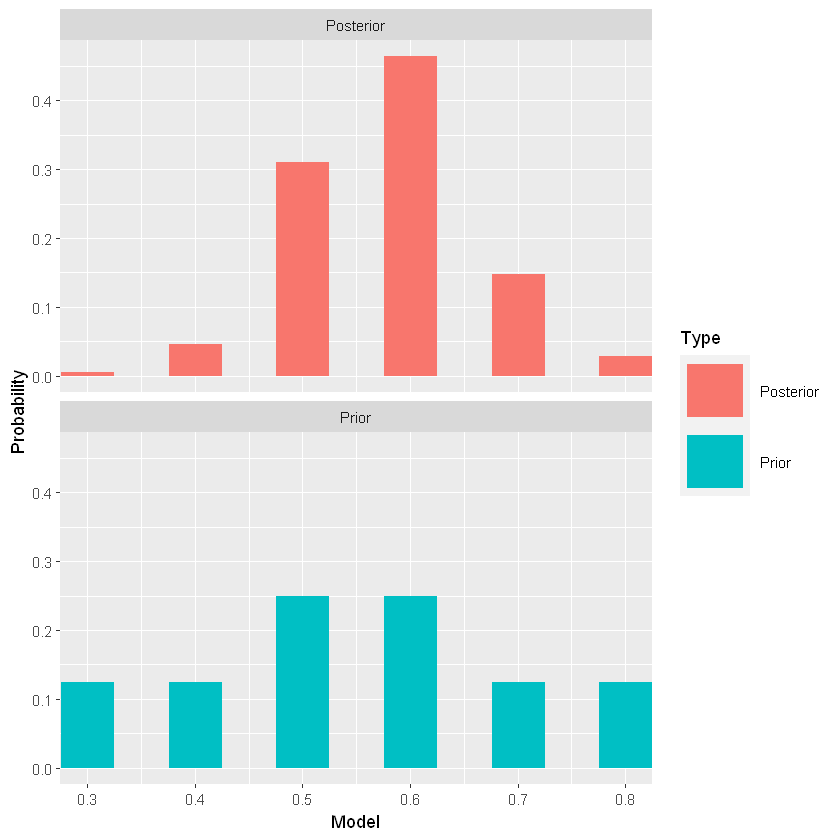
Inferenza Bayesiana
\(P(p>0.5)=?\)
1
| bayes_df %>% select(P, Posterior)
|
A data.frame: 6 × 2
| P | Posterior |
|---|
| <dbl> | <dbl> |
|---|
| 0.3 | 0.00516129 |
| 0.4 | 0.04516129 |
| 0.5 | 0.30967742 |
| 0.6 | 0.46451613 |
| 0.7 | 0.14709677 |
| 0.8 | 0.02838710 |
1
| bayes_df %>% filter(P>0.5) %>% select(Posterior) %>% sum()
|
0.64
Distribuzione a priori continua
Distribuzione a priori (Beta)
\(p^{a-1}(1-p)^{b-1}\) con \(p \in \Re | 0< p< 1\)
Rappresenta la conoscenza a priori su \(p\)
Non è semplice identificare i parametri \(a\) e \(b\).
Per un semplice esempio, ipotizzo \(a=7\) e \(b=10\)
1
2
| # probabilità che il parametro p sia tra 0.8 e 0.4
pbeta(0.8, 7, 10) - pbeta(0.4, 7, 10)
|
0.526926535983103
1
| beta_area(0.4, 0.8, c(7, 10))
|

1
2
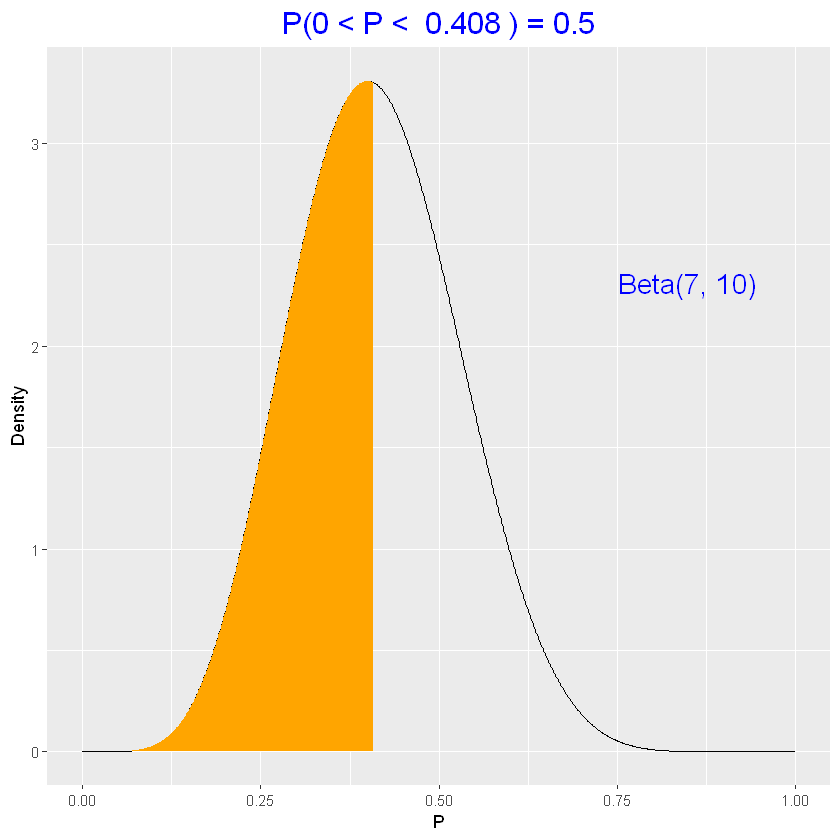
| # il valore mediano risulta
qbeta(0.5, 7, 10)
|
0.408226501324901
1
| beta_quantile(0.5, c(7, 10))
|
Posso determinare una stima dei parametri a priori \(a\) e \(b\), ipotizzando due valori plausibili per il 50-esimo e 90-esimo percentile.
[TO DO] AGGIUNGERE FORMULA PER OTTENERE I PARAMETRI DAI QUANTILI IPOTIZZATI
In base alla propria sensibilità e/o conoscenza di dominio, ipotizzo i due suddetti valori, tenendo presente che, ad esempio, un valore del 90-esimo percentile pari a 0.80, indica che sono sicuro all’90% che \(p\) sia più piccolo di 0.8.
1
2
3
4
5
6
7
| # specifico i quantili 0.5 e 0.9
p50 <- list(x=0.55, p=0.5)
p90 <- list(x=0.80, p=0.9)
# trovo la corrispondente curva beta
parametri_priori <- beta.select(p50, p90)
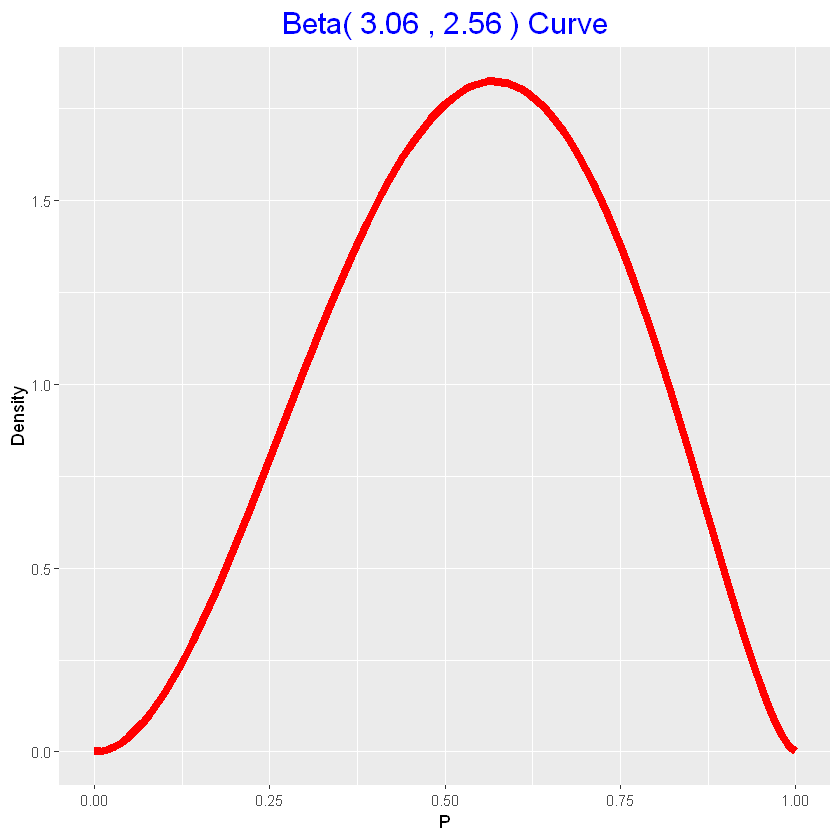
parametri_priori # rispettivamente a e b
|
3.06; 2.56
1
2
| # plot beta a priori
beta_draw(parametri_priori)
|
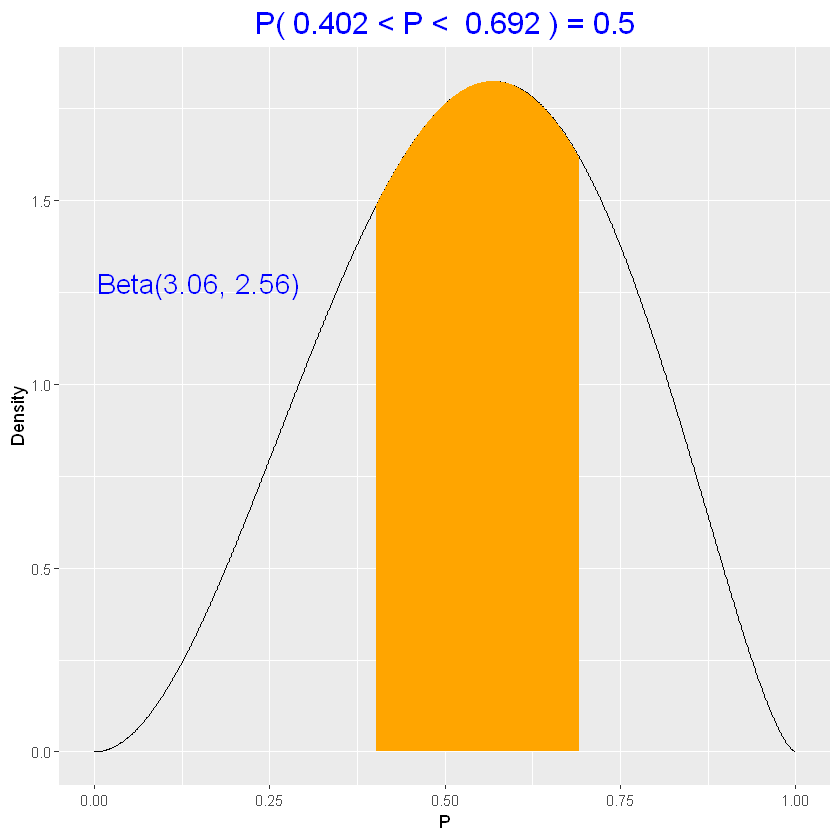
1
2
| # calcolo l'intervallo di probabilità 50%
beta_interval(0.5, parametri_priori)
|
1
2
| # calcolo la probabilità che p sia minore di 0.4
beta_area(0, 0.4, parametri_priori)
|

Verosimiglianza (Binomiale)
A seguito della raccolta empirica dei dati da un campione, si ottengono 12 positivi su 20.
L’esperimento è binomiale: la probabilità di 12 successi su 20, con probabilità di successo \(p\)
\(L={20\choose 12}p^{12}(1-p)^{8}\)
Distribuzione a posteriori (Beta)
\(\mbox{Posteriori}\propto \mbox{Prori} \times \mbox{Verosimiglianza}\)
\(\mbox{Posteriori}\propto [p^{3.06}(1-p)^{2.56-1}]\times [p^{12}(1-p)^8]=p^{15.06-1}(1-p)^{10.56-1}\equiv \mbox{Densità }\mathrm{B}(15.06,10.56)\)
Quindi si ha
\(\bigg\{\mbox{Priori}=\mathrm{B}\big(a,b\big)\bigg\}\times \bigg\{\mbox{Verosimiglianza}=\mathrm{Bin}\Big(p=\frac{s}{s+f}\Big)\bigg\}=\bigg\{\mbox{Posteriori}=\mathrm{B}\big(a+s,b+f\big)\bigg\}\)
1
2
3
| data <- c(12,8)
parametri_posteriori <- parametri_priori + data
parametri_posteriori
|
15.06; 10.56
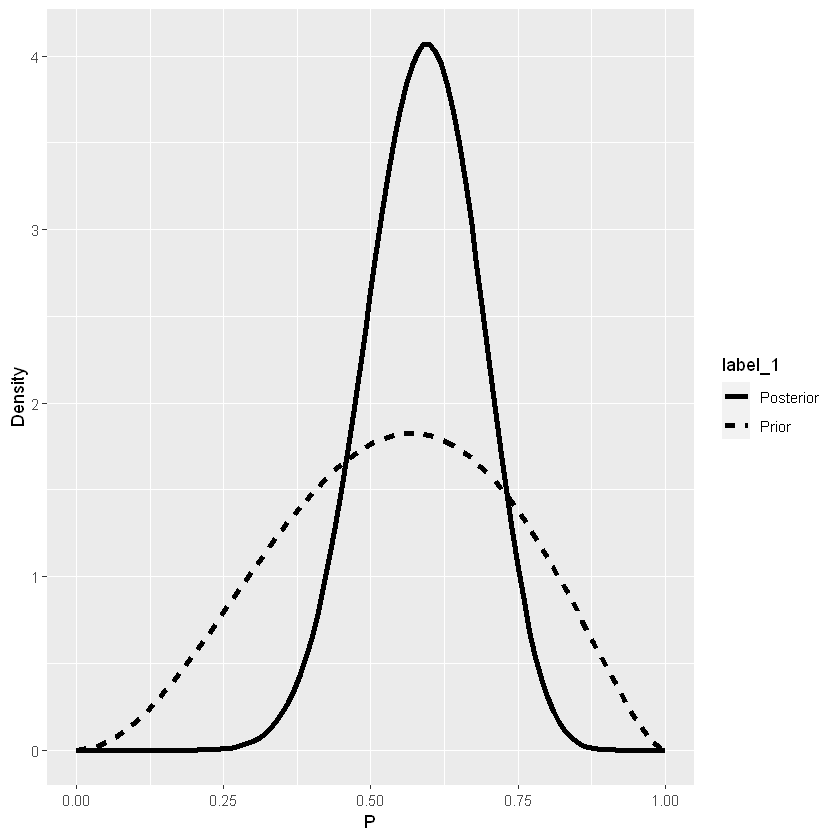
1
2
| # confronto priori e posteriori
beta_prior_post(parametri_priori, parametri_posteriori)
|
Inferenza Bayesiana
Test d’ipotesi
Valutiamo l’ipotesi che l’80% è positivo
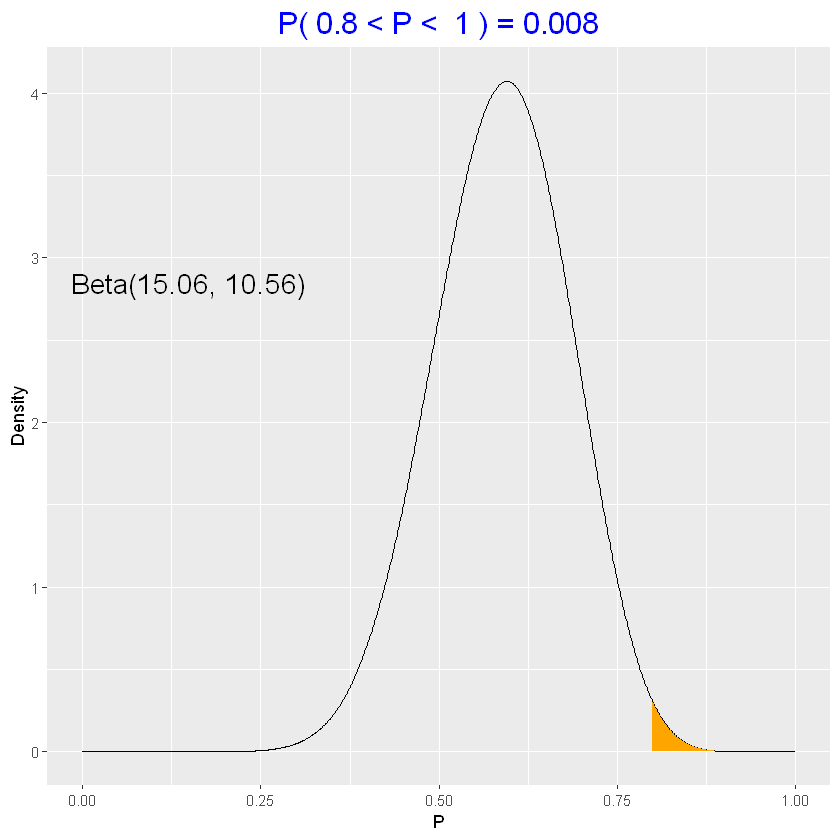
\(H:P>0.80\)
1
| 1 - pbeta(0.8, parametri_posteriori[1], parametri_posteriori[2])
|
0.00818530232747894
1
| beta_area(0.8, 1, parametri_posteriori)
|
Intervalli di credibilità
Un intervallo di credibilità al 90%, è un intervallo che contiene al 90% la probabilità di contenere il parametro.
1
2
| # intervallo equi-tails
beta_interval(0.90, parametri_posteriori)
|
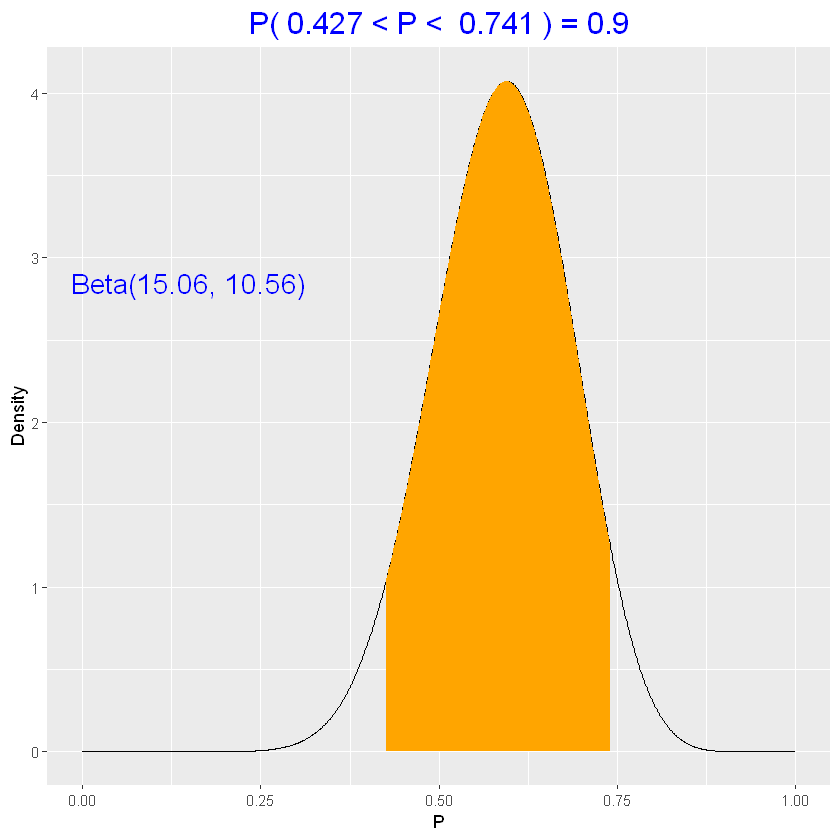
La probabilità che \(p\) sia nell’intervallo \((0.427,0.741)\) è esattamente 0.9.
Intervalli di confidenza
Nell’approccio classico (frequentista), l’intervallo di confidenza è basato sulla condizione degli esperimenti ripetuti.
Secondo il metodo “aggiungi 2 successi e 2 insuccessi” di Agresti e Coull, dati \(y\) successi e un campione di dimensione \(n\), l’intervallo 90% è:
\((\hat{p}-1.645se,\hat{p}+1.645se)\)
con
\(\hat{p}=\frac{y+2}{n+4}\) e \(se=\sqrt{\frac{\hat{p}(1-\hat{p})}{n+4}}\)
1
| classical_binom_ci(12, 20, 0.90)
|
0.417804211107709; 0.748862455558958
L’intervallo bayesiano è più stretto dell’intervallo di confidenza, è prevedibile in quanto è più preciso perché combina i dati con l’informazione a priori.
Simulazioni dalla a-posteriori
1
2
| # genero 1000 osservazioni dalla densità beta con i parametri precedenti
sim_p <- rbeta(1000, parametri_posteriori[1], parametri_posteriori[2])
|
1
2
3
| # valuto la loro distribuzione
hist(sim_p, freq=FALSE)
curve(dbeta(x, parametri_posteriori[1], parametri_posteriori[2]), add=TRUE, col="red", lwd=3)
|

1
2
3
| # probabilità che p < 0.5 usando la simulazione
prob <- sum(sim_p < 0.5)/1000
prob
|
0.192
1
2
| # probabilità esatta
pbeta(0.5, parametri_posteriori[1], parametri_posteriori[2])
|
0.182415035367533
1
2
| # quantili campionari
quantile(sim_p, c(0.05, 0.95))
|
5%: 0.425741818823082; 95%: 0.737247520104539
Posterior of log odds ratio
Vogliamo ottenere l’intervallo al 90% di probabilità per \(\log{\frac{p}{1-p}}\)
1
| sim_logit <- log(sim_p / (1-sim_p))
|
1
2
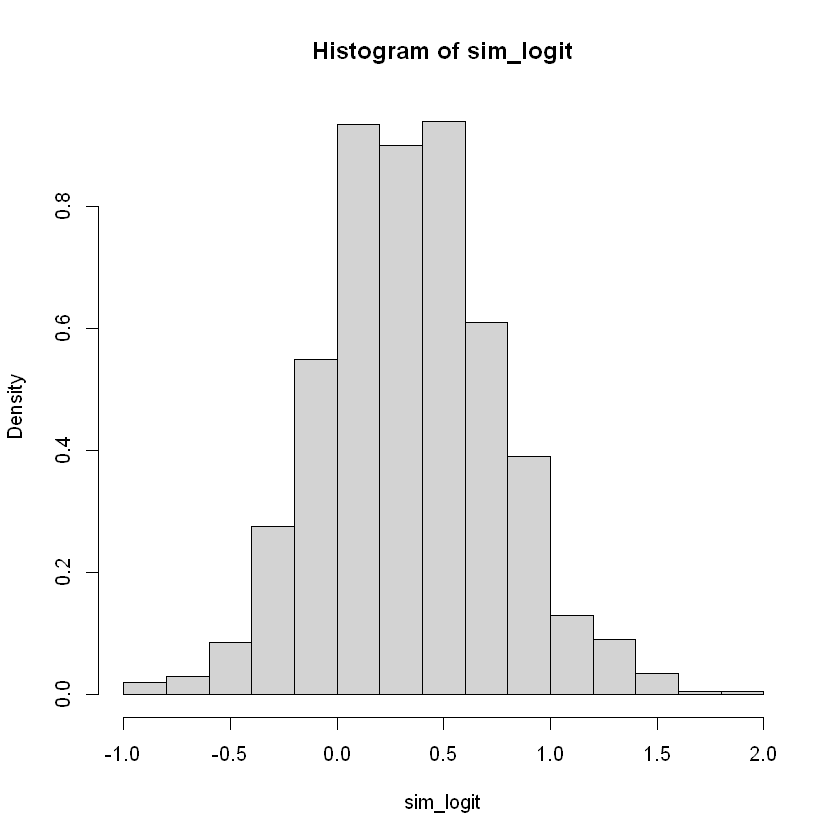
| # distribuzione
hist(sim_logit, freq=FALSE)
|
1
2
| # quantili campionari
quantile(sim_logit, c(0.10, 0.90))
|
10%:-0.15169200371894; 90%:0.86935740076806
1
2
| # clear environment
rm(list=ls())
|
Normal sampling model (\(\sigma\) noto)
Sia \(M\) una v.a. che modella i secondi necessari per calciare un rigore.
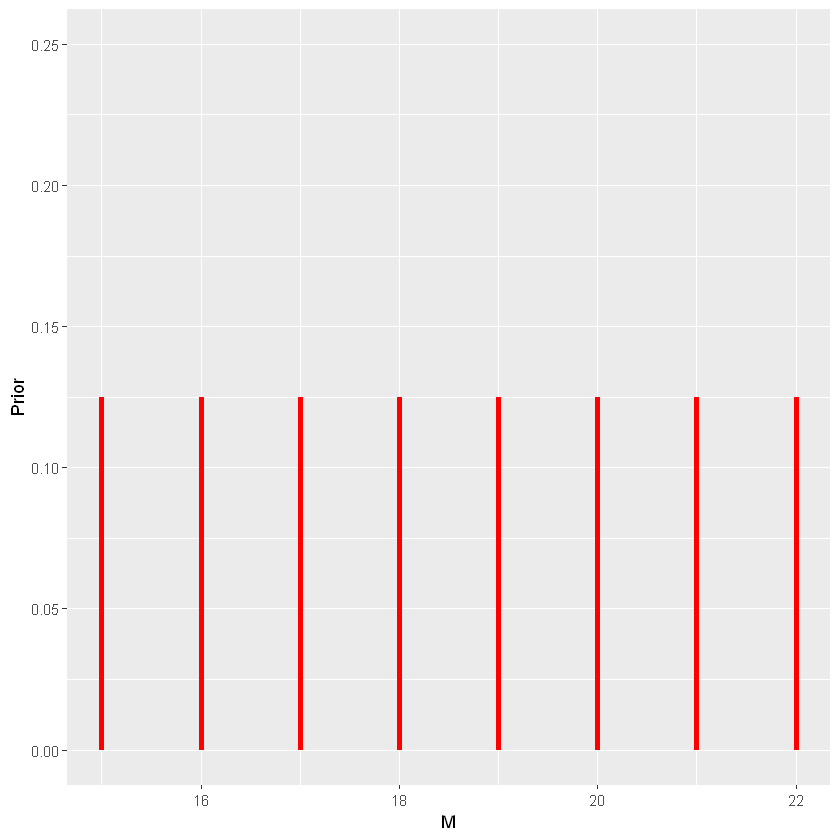
Ipotizzo un range tra 15 e 22 secondi, distribuito uniformemente (discreto).
\(M\sim\mathrm{U}[15,22]\)
1
2
| bayes_df <- data.frame(M=15:22,Prior=rep(1/8,8))
prob_plot(bayes_df) + ylim(0,0.25)
|
Verosimiglianza (Normale)
1
2
3
4
| # verosimiglianze "plausibili"
Models <- list(c(15,4), c(16,4), c(17,4), c(18,4),
c(19,4), c(20,4), c(21,4), c(22,4))
many_normal_plots(Models)
|

Si registrano 20 tiri in porta e si osserva che
il valore medio \(\hat{y}=17.2\)
lo standard error associato \(se=\frac{S}{\sqrt{n}}=\frac{4}{\sqrt{20}}=0.89\)
1
2
3
4
5
| # collect data
ymean <- 17.2
se <- 4/sqrt(20)
bayes_df$Likelihood <- dnorm(ymean, mean=bayes_df$M, sd=se)
round(bayes_df, 3)
|
A data.frame: 8 × 3
| M | Prior | Likelihood |
|---|
| <dbl> | <dbl> | <dbl> |
|---|
| 15 | 0.125 | 0.022 |
| 16 | 0.125 | 0.181 |
| 17 | 0.125 | 0.435 |
| 18 | 0.125 | 0.299 |
| 19 | 0.125 | 0.059 |
| 20 | 0.125 | 0.003 |
| 21 | 0.125 | 0.000 |
| 22 | 0.125 | 0.000 |
Distribuzione a posteriori (Normale)
1
2
3
| # calcolo posteriori
bayes_df <- bayesian_crank(bayes_df)
round(bayes_df,3)
|
A data.frame: 8 × 5
| M | Prior | Likelihood | Product | Posterior |
|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
|---|
| 15 | 0.125 | 0.022 | 0.003 | 0.022 |
| 16 | 0.125 | 0.181 | 0.023 | 0.181 |
| 17 | 0.125 | 0.435 | 0.054 | 0.435 |
| 18 | 0.125 | 0.299 | 0.037 | 0.299 |
| 19 | 0.125 | 0.059 | 0.007 | 0.059 |
| 20 | 0.125 | 0.003 | 0.000 | 0.003 |
| 21 | 0.125 | 0.000 | 0.000 | 0.000 |
| 22 | 0.125 | 0.000 | 0.000 | 0.000 |
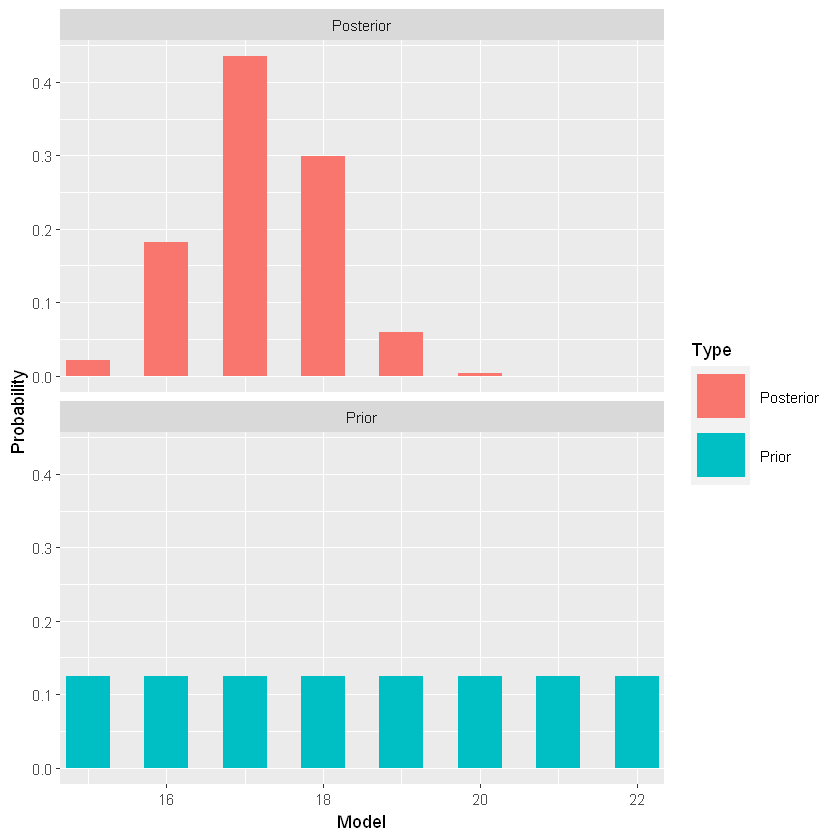
1
2
| # priori vs posteriori
prior_post_plot(bayes_df)
|
1
2
3
4
5
6
7
8
9
10
11
12
| # quali range di valori ha almeno il 90% di probabilità
bayes_df %>%
arrange(desc(Posterior)) %>%
select(M, Posterior) %>%
head(3) %>%
mutate(
Posterior = round(Posterior,3),
M = as.character(M)
) %>%
as.data.frame() %>%
# bind_rows(data.frame(M="Totale",Posterior=sum(.[,"Posterior"])))
bind_rows(summarise_all(., ~ if (is.numeric(.)) sum(.) else "Totale"))
|
A data.frame: 4 × 2
| M | Posterior |
|---|
| <chr> | <dbl> |
|---|
| 17 | 0.435 |
| 18 | 0.299 |
| 16 | 0.181 |
| Totale | 0.915 |
Distribuzione a priori (Normale)
Assumiamo ora che la distribuzione a priori sia continua e segua una normale.
\(\mathscr{N}(M_0,S_0)\)
Con \(M_0\) rappresenta la migliore ipotesi di \(M\) e \(S_0\) indica quanto sono sicuro della ipotesi.
Un esperto suggerisce che \(M\) sia vicino a 18 secondi, e si avrà un valore piccolo per \(S_0\) (es \(0.1\)).
Un inesperto pensa che \(M\) sia vicino a 18 secondi, ma si avrà un valore elevato per \(S_0\) (es \(7\)).
Posso determinare una stima dei parametri a priori \(M_0\) e \(S_0\), ipotizzando due valori plausibili per il 50-esimo e 90-esimo percentile.
[TO DO] AGGIUNGERE FORMULA PER OTTENERE I PARAMETRI DAI QUANTILI IPOTIZZATI
Il quantile è un valore di \(M\) che indica la possibilità di essere inferiore di quel valore con una data probabilità.
In base alla propria sensibilità e/o conoscenza di dominio, ipotizzo i due suddetti valori
- \(0.50\) quantile per M è \(18\) secondi (significa che è ugualmente probabile che un valore sia più alto o più basso di \(18\) secondi)
- \(0.90\) quantile per M è \(20\) secondi (significa che la probabilità di ottenere un valore inferiore a \(20\) è del 90%)
1
2
3
4
| # stima parametri dall'assegnazione di due quantili
parametri_priori <- lapply(normal.select(list(x=18, p=0.5),
list(x=20, p=0.9)), function(x) round(x, 2))
parametri_priori
|
- $mu
- 18
- $sigma
- 1.56
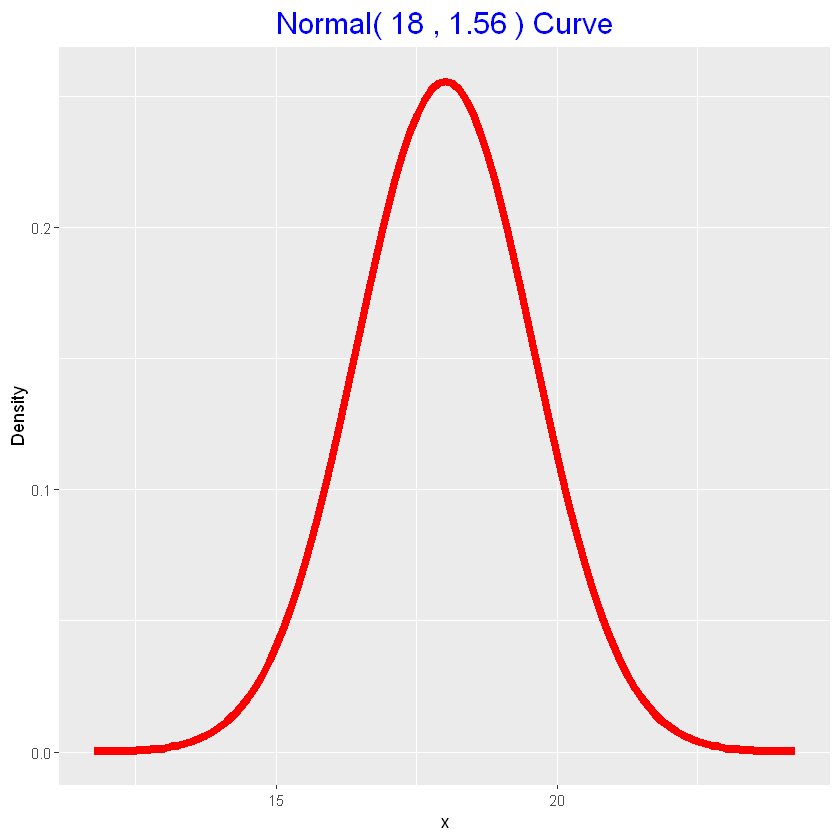
1
2
| # distribuzione a priori
normal_draw(parametri_priori)
|
1
2
| # trovo il quantile 0.25 della priori
qnorm(0.25, parametri_priori$mu, parametri_priori$sigma)
|
16.9477959896941
1
| normal_quantile(0.25, parametri_priori)
|
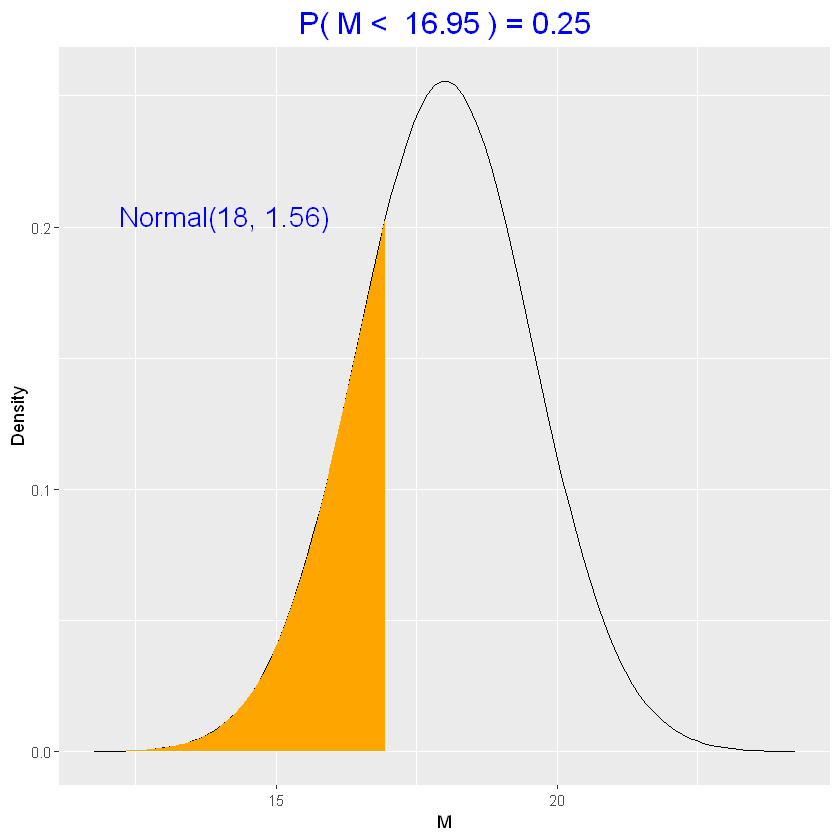
è ragionevole che \(P(M<16.95)=0.25\)? Se no, si perfezionano \(M_0\) e \(S_0\)
1
2
3
4
5
| # assegno distribuzione a priori
bayes_df <- data.frame(M=15:22)
bayes_df <- bayes_df %>%
mutate(Prior=round(dnorm(M, mean=parametri_priori$mu, sd=parametri_priori$sigma),3))
bayes_df
|
A data.frame: 8 × 2
| M | Prior |
|---|
| <int> | <dbl> |
|---|
| 15 | 0.040 |
| 16 | 0.112 |
| 17 | 0.208 |
| 18 | 0.256 |
| 19 | 0.208 |
| 20 | 0.112 |
| 21 | 0.040 |
| 22 | 0.010 |
Verosimiglianza (Normale)
Si registrano 20 tiri in porta e si osserva che
il valore medio \(\hat{y}=17.2\)
lo standard error associato \(se=\frac{S}{\sqrt{n}}=\frac{4}{\sqrt{20}}=0.89\)
1
2
3
4
5
| # verosimiglianza
parametri_verosimiglianza <- list(mu=17.2, sigma=0.89)
bayes_df <- bayes_df %>%
mutate(Likelihood=dnorm(parametri_verosimiglianza$mu, mean=M, sd=parametri_verosimiglianza$sigma))
round(bayes_df,3)
|
A data.frame: 8 × 3
| M | Prior | Likelihood |
|---|
| <dbl> | <dbl> | <dbl> |
|---|
| 15 | 0.040 | 0.021 |
| 16 | 0.112 | 0.181 |
| 17 | 0.208 | 0.437 |
| 18 | 0.256 | 0.299 |
| 19 | 0.208 | 0.058 |
| 20 | 0.112 | 0.003 |
| 21 | 0.040 | 0.000 |
| 22 | 0.010 | 0.000 |
Distribuzione a posteriori (Normale)
\(\mbox{Posteriori}\propto \mbox{Prori} \times \mbox{Verosimiglianza}\)
Quindi si ha
\(\bigg\{\mbox{Priori}=\mathscr{N}\big(M_0,S_0\big)\bigg\}\times \bigg\{\mbox{Verosimiglianza}=\mathscr{N}\big(M_1,S_1\big)\bigg\}=\bigg\{\mbox{Posteriori}=\mathscr{N}\big(M_{Post},S_{Post}\big)\bigg\}\)
con
\(P_k=\frac{1}{S_k^2}\)
\(M_{Post}=\mbox{W.AVG}(M;P)\)
\(S_{Post}=\frac{1}{\sqrt{\sum S}}\)
1
2
3
| # aggiungo la precision ai parametri a priori
parametri_priori <- append(parametri_priori, list(precision=round(1/parametri_priori$sigma^2,2)))
parametri_priori
|
- $mu
- 18
- $sigma
- 1.56
- $precision
- 0.41
1
2
3
| # parametri verosimiglianza, con la sua precision
parametri_verosimiglianza <- append(parametri_verosimiglianza, list(precision=round(1/parametri_verosimiglianza$sigma^2,2)))
parametri_verosimiglianza
|
- $mu
- 17.2
- $sigma
- 0.89
- $precision
- 1.26
1
2
3
4
5
6
7
8
9
10
11
| # parametri posteriori, con la sua precision
parametri_posteriori <- list(
mu = round(weighted.mean(x=c(parametri_priori$mu,
parametri_verosimiglianza$mu),
w=c(parametri_priori$precision,
parametri_verosimiglianza$precision)),2),
sigma = round(1/sqrt(sum(c(parametri_priori$precision,
parametri_verosimiglianza$precision))),2),
precision = sum(c(parametri_priori$precision,
parametri_verosimiglianza$precision)))
parametri_posteriori
|
- $mu
- 17.4
- $sigma
- 0.77
- $precision
- 1.67
1
2
3
4
5
6
| # dati insieme
rbind(
data.frame(fonte="parametri_priori",parametri_priori),
data.frame(fonte="parametri_verosimiglianza",parametri_verosimiglianza),
data.frame(fonte="parametri_posteriori",parametri_posteriori)
)
|
A data.frame: 3 × 4
| fonte | mu | sigma | precision |
|---|
| <chr> | <dbl> | <dbl> | <dbl> |
|---|
| parametri_priori | 18.0 | 1.56 | 0.41 |
| parametri_verosimiglianza | 17.2 | 0.89 | 1.26 |
| parametri_posteriori | 17.4 | 0.77 | 1.67 |
1
2
3
| # funzione automatica calcolo posteriori normale
normal_update(as.numeric(parametri_priori[1:2]),
as.numeric(parametri_verosimiglianza[1:2]))
|
17.3964472827603; 0.773041159419683
1
2
3
4
| # funzione automatica (estesa) calcolo posteriori normale
normal_update(as.numeric(parametri_priori[1:2]),
as.numeric(parametri_verosimiglianza[1:2]),
teach=TRUE)
|
A data.frame: 3 × 4
| Type | Mean | Precision | Stand_Dev |
|---|
| <chr> | <dbl> | <dbl> | <dbl> |
|---|
| Prior | 18.00000 | 0.4109139 | 1.5600000 |
| Data | 17.20000 | 1.2624669 | 0.8900000 |
| Posterior | 17.39645 | 1.6733807 | 0.7730412 |
1
2
3
| # confronto grafico tra priori e posteriori
many_normal_plots(list(as.numeric(parametri_priori[1:2]),
as.numeric(parametri_posteriori[1:2])))
|

Inferenza Bayesiana
Test d’ipotesi
Valutiamo l’ipotesi che servano in media almeno 19 secondi per calciare
\(H:M\ge 19\)
Approccio classico
Test statistics \(Z=\frac{\bar{y}-19}{se}\)
1
2
3
| # Z score
z <- (parametri_verosimiglianza$mu - 19)/parametri_verosimiglianza$sigma
z
|
-2.02247191011236
1
2
| # p-value del z-score
pnorm(z)
|
0.0215638113390887
Con l’approccio classico si ha un p-value del 2% e si riufiuta l’ipotesi nulla.
Approccio Bayesiano
L’attuale opinione è rappresentata dalla posteriori
\(\mathscr{N}(17.4,0.77)\)
1
2
| # probabilità che M>=19
1 - pnorm(19, parametri_posteriori$mu, parametri_posteriori$sigma)
|
0.0188582683438657
Ottengo un risultato simile al p-value, e anche in questo caso si rifiuta l’ipotesi nulla, o meglio dire che l’affermazione ipotizzata è improbabile che sia vera.
Simulazioni dalla a-posteriori
Siamo interessati a conoscere il tempo medio (e un suo intervallo di credibilità)
1
2
| # distribuzione a posteriori
normal_draw(parametri_posteriori)
|
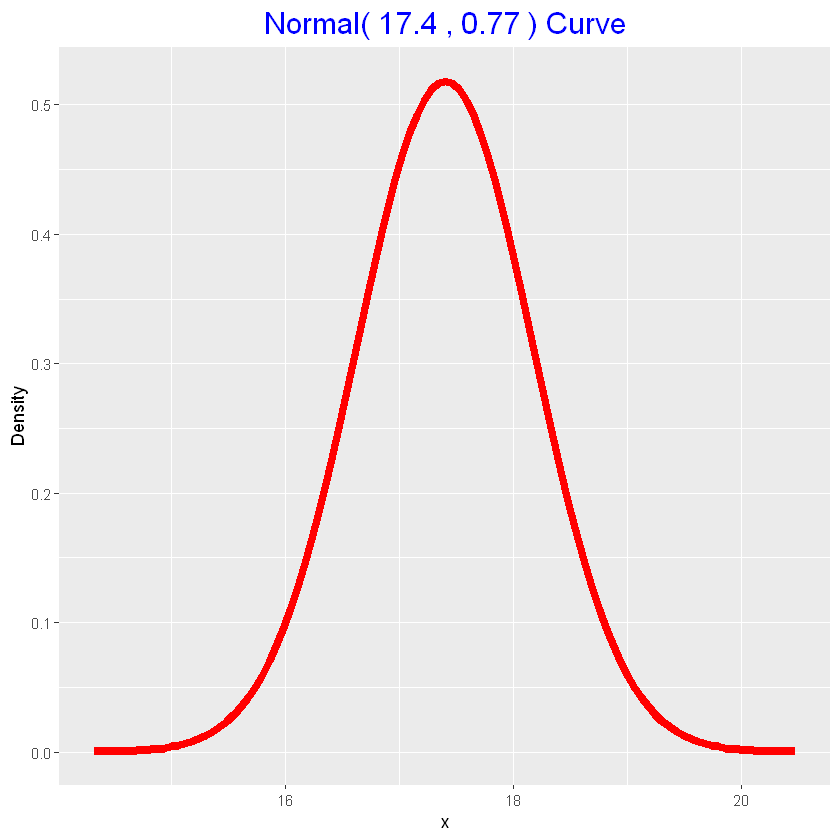
1
2
| # simulation
M_sim <- rnorm(1000, mean=parametri_posteriori$mu, sd=parametri_posteriori$sigma)
|
1
2
3
4
| # intervallo di credibilità a 80%
# round(quantile(M_sim, c(0.10, 0.90)),1)
normal_interval(0.80, parametri_posteriori)
# la probabilità che M sia in questo intervallo è dell'80%
|
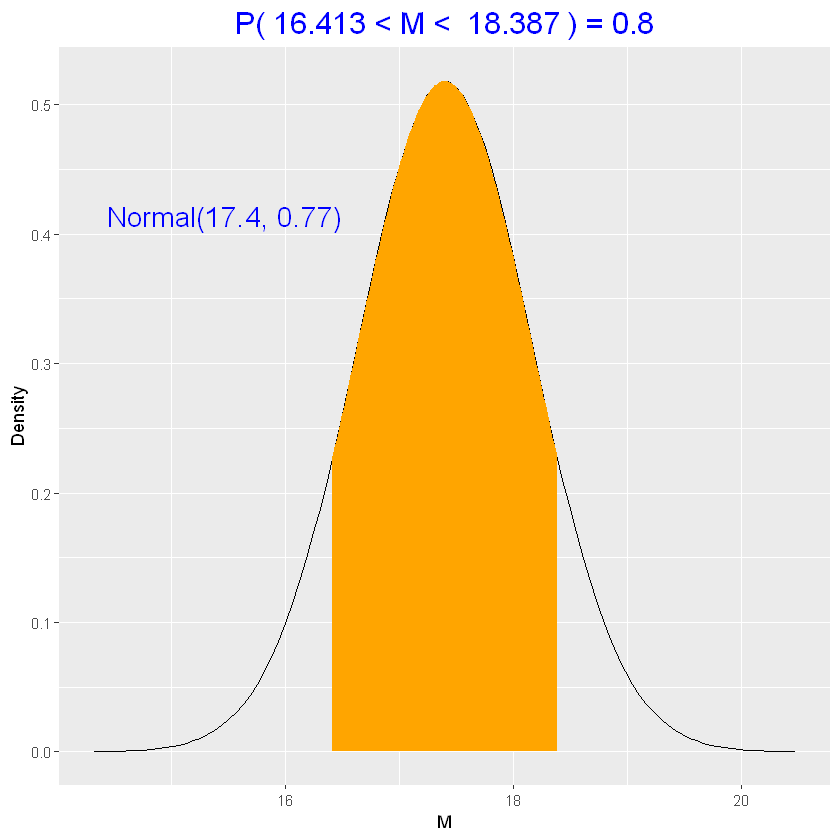
Bayesian Predictions
Per prevedere il prossimo tempo \(y\) serve determinare la predictive density di \(y\).
Non conosciamo il vero valore di \(M\) ma conosciamo la distribuzione a posteriori \(\mathscr{N}(17.4,0.77)\)
Step
- si simula un valore \(M\) da \(\mathscr{N}(17.4,0.77)\)
- si simula un valore \(y\) dalla densità \(\mathscr{N}(M,4)\), in questo caso il valore \(4\) è stato ipotizzato
1
2
| # simulazione dalla posteriori
M_sim <- rnorm(1000, mean=parametri_posteriori$mu, sd=parametri_posteriori$sigma)
|
1
2
| # simulazione dalla densità predittiva
y_sim <- rnorm(1000, mean=M_sim, sd=4)
|
1
2
| # intervallo di credibilità previsto all'80%
round(quantile(y_sim, c(0.10, 0.90)), 1)
|
10%:11.8; 90%:22.6
L’intervallo di credibilità all’80% è più stretto dell’intervallo di credibilità previsto, in quanto non si conosce il valore di \(M\) (inference) né il valore di \(y\vert M\) (sampling).
Bivariate Bayesian Testing
Inferenza Bayesiana
Siano \(p_W\) e \(p_M\) le proporzioni di donne e uomini positivi.
Test d’ipotesi
- Ipotesi 1 \(p_W>p_M\)
- Ipotesi 2 \(p_W=p_M\)
Distribuzione a priori (proporzioni)
In un approccio discreto, un modello è una coppia \((p_W,p_M)\)
Ipotizzo una distribuzione discreta, con range tra \(0.1\) e \(0.9\) (quindi \(9\times 9\) possibili modelli).
La distribuzione è descrive la relazione tra le due proporzioni
- \(P(p_W=p_M)=0.5\) (diagonale)
- \(P(p_W\neq p_M)=0.5\) (fuori la diagonale)
1
2
3
| # distribuzione test-priori
prior <- testing_prior(lo=0.1, hi=0.9, n_values=9, pequal=0.5)
round(prior, 3)
|
A matrix: 9 × 9 of type dbl
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|
| 0.1 | 0.056 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 |
|---|
| 0.2 | 0.007 | 0.056 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 |
|---|
| 0.3 | 0.007 | 0.007 | 0.056 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 |
|---|
| 0.4 | 0.007 | 0.007 | 0.007 | 0.056 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 |
|---|
| 0.5 | 0.007 | 0.007 | 0.007 | 0.007 | 0.056 | 0.007 | 0.007 | 0.007 | 0.007 |
|---|
| 0.6 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.056 | 0.007 | 0.007 | 0.007 |
|---|
| 0.7 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.056 | 0.007 | 0.007 |
|---|
| 0.8 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.056 | 0.007 |
|---|
| 0.9 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.056 |
|---|
1
2
| # plot della test-priori
draw_two_p(prior)
|
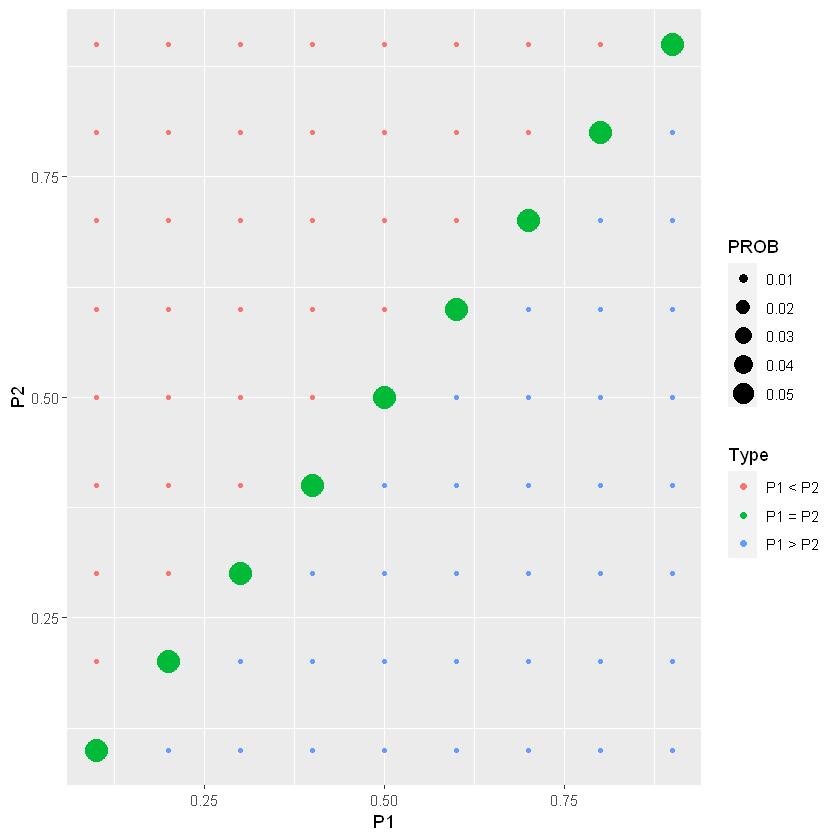
Verosimiglianza (Binomiale)
Si osservano 10 donne e 14 uomini positivi.
Si possono assumere campioni indipendenti e con distribuzione binomiale, quindi la verosimiglianza è il prodotto (vettoriale) delle densità binomiali
1
2
3
4
5
6
7
| pW <- seq(0.1,0.9,by=0.1)
pM <- seq(0.1,0.9,by=0.1)
# outer è il prodotto tra vettore riga e colonna (nx1 * 1xn = nxn)
# a %*% t(b)
Likelihood <- outer(dbinom(10, size=20, prob=pW),
dbinom(14, size=20, prob=pM))
round(Likelihood,3)
|
A matrix: 9 × 9 of type dbl
| 0 | 0 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0 | 0 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0 | 0 | 0 | 0.000 | 0.001 | 0.004 | 0.006 | 0.003 | 0.000 |
| 0 | 0 | 0 | 0.001 | 0.004 | 0.015 | 0.022 | 0.013 | 0.001 |
| 0 | 0 | 0 | 0.001 | 0.007 | 0.022 | 0.034 | 0.019 | 0.002 |
| 0 | 0 | 0 | 0.001 | 0.004 | 0.015 | 0.022 | 0.013 | 0.001 |
| 0 | 0 | 0 | 0.000 | 0.001 | 0.004 | 0.006 | 0.003 | 0.000 |
| 0 | 0 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0 | 0 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
Distribuzione a posteriori (proporzioni)
\(\mbox{Posteriori}=\frac{\mbox{Prori} \times \mbox{Verosimiglianza}}{\sum\big(\mbox{Prori} \times \mbox{Verosimiglianza}\big)}\)
1
2
3
| # posterior <- prior*Likelihood/sum(prior*Likelihood)
posterior <- two_p_update(prior, c(10,10), c(14,6))
round(posterior,3)
|
A matrix: 9 × 9 of type dbl
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|
| 0.1 | 0 | 0 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
|---|
| 0.2 | 0 | 0 | 0 | 0.000 | 0.000 | 0.001 | 0.001 | 0.001 | 0.000 |
|---|
| 0.3 | 0 | 0 | 0 | 0.000 | 0.003 | 0.009 | 0.014 | 0.008 | 0.001 |
|---|
| 0.4 | 0 | 0 | 0 | 0.011 | 0.010 | 0.035 | 0.053 | 0.030 | 0.002 |
|---|
| 0.5 | 0 | 0 | 0 | 0.002 | 0.124 | 0.052 | 0.080 | 0.046 | 0.004 |
|---|
| 0.6 | 0 | 0 | 0 | 0.001 | 0.010 | 0.277 | 0.053 | 0.030 | 0.002 |
|---|
| 0.7 | 0 | 0 | 0 | 0.000 | 0.003 | 0.009 | 0.112 | 0.008 | 0.001 |
|---|
| 0.8 | 0 | 0 | 0 | 0.000 | 0.000 | 0.001 | 0.001 | 0.004 | 0.000 |
|---|
| 0.9 | 0 | 0 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
|---|
1
2
| # plot
draw_two_p(posterior)
|
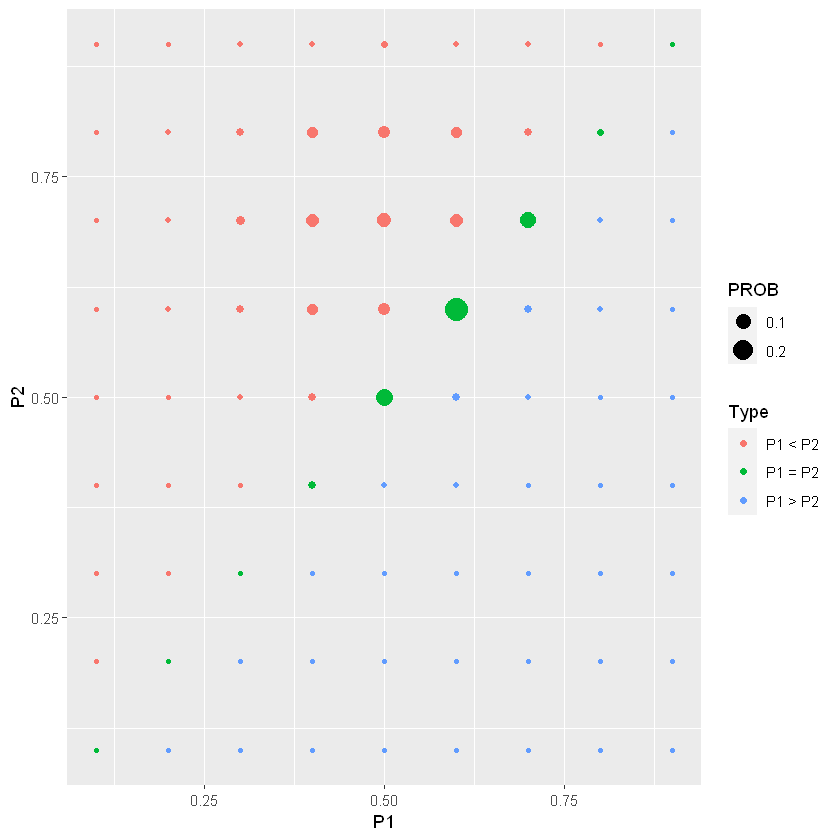
Analisi delle differenze
Trasformo la matrice \(9\times 9\) in una matrice \(81\times 2\), ottengo le differenze tra \(p_W\) e \(p_M\), raggruppo per tale differenza sommando le probabilità (le due colonne hanno 9 valori, quindi 17 combinazioni).
Analizzo la distribuzione delle differenze tra le due proporzioni
\(d=p_M-p_W\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| # differenze e probabilità
# tabella <- as.matrix(posterior)
# tabella <- data.frame(
# diff21 = as.vector(outer(colnames(tabella), rownames(tabella), FUN=function(x,y) round(as.numeric(y)-as.numeric(x),1))),
# Prob = as.vector(tabella)
# )
# d <- tabella %>%
# group_by(diff21) %>%
# summarise(Prob = sum(Prob), .groups = 'drop_last')
d <- two_p_summarize(posterior)
d %>% head() %>% round(3)
|
A tibble: 6 × 2
| diff21 | Prob |
|---|
| <dbl> | <dbl> |
|---|
| -0.8 | 0.000 |
| -0.7 | 0.000 |
| -0.6 | 0.000 |
| -0.5 | 0.000 |
| -0.4 | 0.000 |
| -0.3 | 0.001 |
1
2
| # plot differenze
prob_plot(d)
|

Con la distribuzione a priori ho assunto che si ha il 50% di probabilità di ottenere proporzioni uguali (differenza nulla).
L’a posteriori mostra che la \(P(\mbox{d}=0)\) è elevata, ma è discreta la probabilità che la proporzione degli uomini sia maggiore rispetto quella delle donne.
1
2
| # Posteriori: P(diff<0==p_W>p_M)
d %>% filter(diff21<0) %>% select(Prob) %>% sum() %>% round(3)
|
0.028
1
2
| # Priori: P(diff<0==p_W>p_M)
sum(prior[upper.tri(prior)])
|
0.25
1
2
| # Posteriori: P(diff=0==p_W=p_M)
d %>% filter(diff21==0) %>% select(Prob) %>% sum() %>% round(3)
|
0.528
1
2
| # Priori: P(diff=0==p_W=p_M)
sum(diag(prior))
|
0.5
Distribuzione a priori (Beta)
Assumiamo che una curva beta rappresenti la conoscenza riguardo \(p_W\) e un’altra riguardo \(p_M\) e che siano indipendenti.
\(p_W \sim \mathrm{B}(1,1)\)
\(p_M \sim \mathrm{B}(1,1)\)
1
2
3
| # genero dalla priori
df <- data.frame(pW=rbeta(1000,1,1), pM=rbeta(1000,1,1))
ggplot(df, aes(pW,pM)) + geom_point() + xlim(0,1) + ylim(0,1)
|
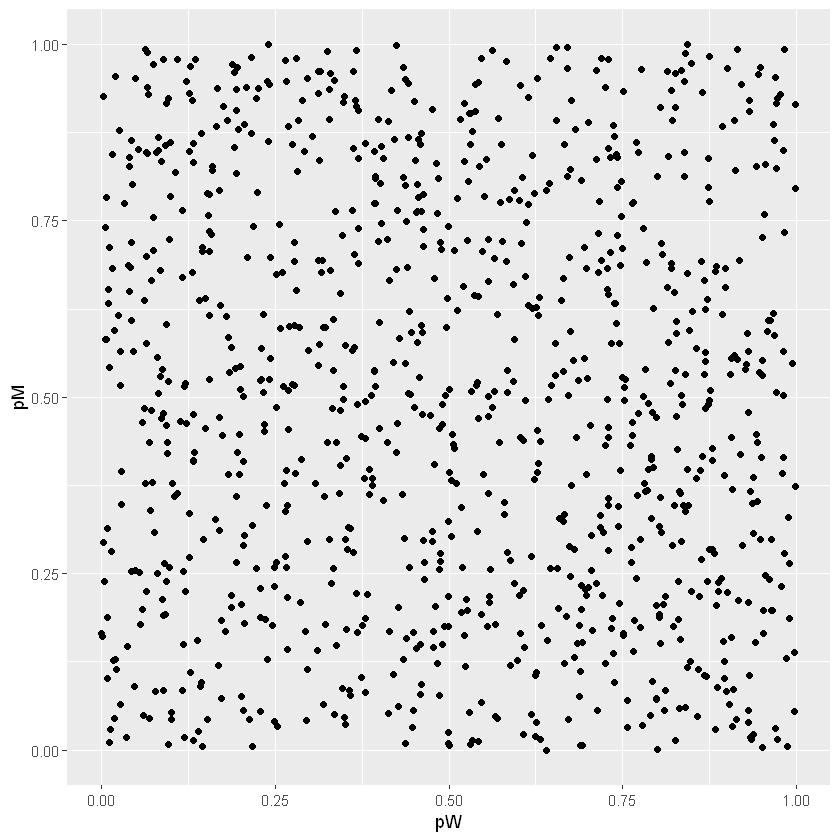
Verosimiglianza (Binomiale)
Si osservano 10 donne e 14 uomini positivi.
Si possono assumere campioni indipendenti e con distribuzione binomiale, quindi la verosimiglianza è il prodotto (vettoriale) delle densità binomiali
Distribuzione a posteriori (Beta)
Sarà una \(\mathrm{B}(p_W,p_M)\)
\(p_W \sim \mathrm{B}(10+1,10+1)\)
\(p_M \sim \mathrm{B}(14+1,6+1)\)
[TO DO] DA DETERMINARE ANALITICAMENTE L’A POSTERIORI
1
2
3
| # simulo pW e pM
pW <- rbeta(1000, 11, 11)
pM <- rbeta(1000, 15, 7)
|
1
2
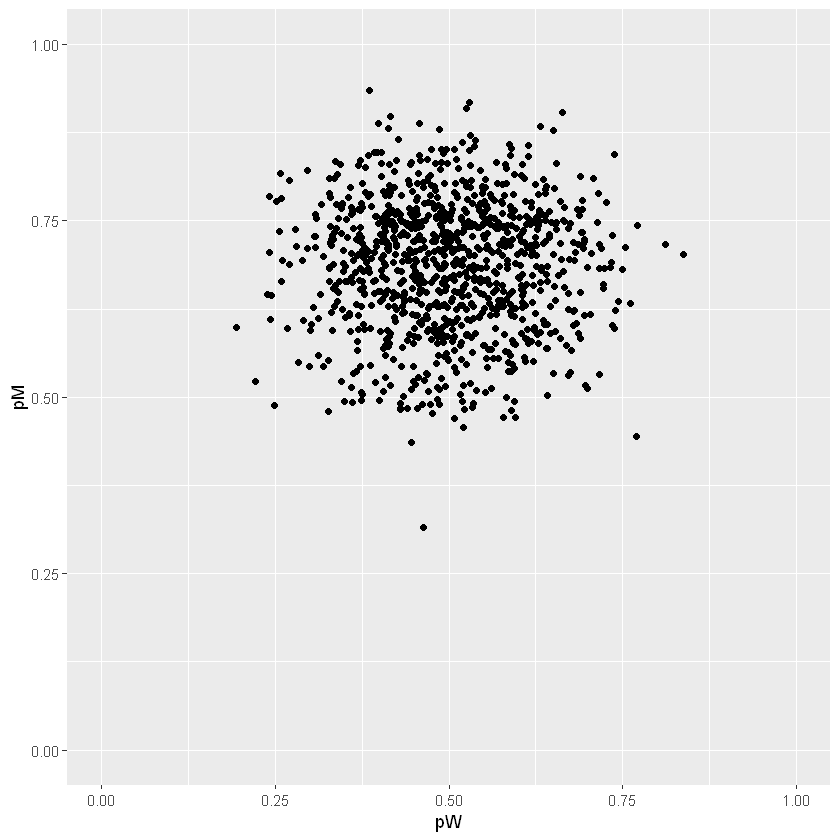
3
| # plot posteriori
df <- data.frame(pW, pM)
ggplot(df, aes(pW,pM)) + geom_point() + xlim(0,1) + ylim(0,1)
|
1
2
| # prob pW<pM
with(df, sum(pW<pM)/1000)
|
0.898
1
2
| # differenza posteriori
df$d_21 <- with(df, pM-pW)
|
1
2
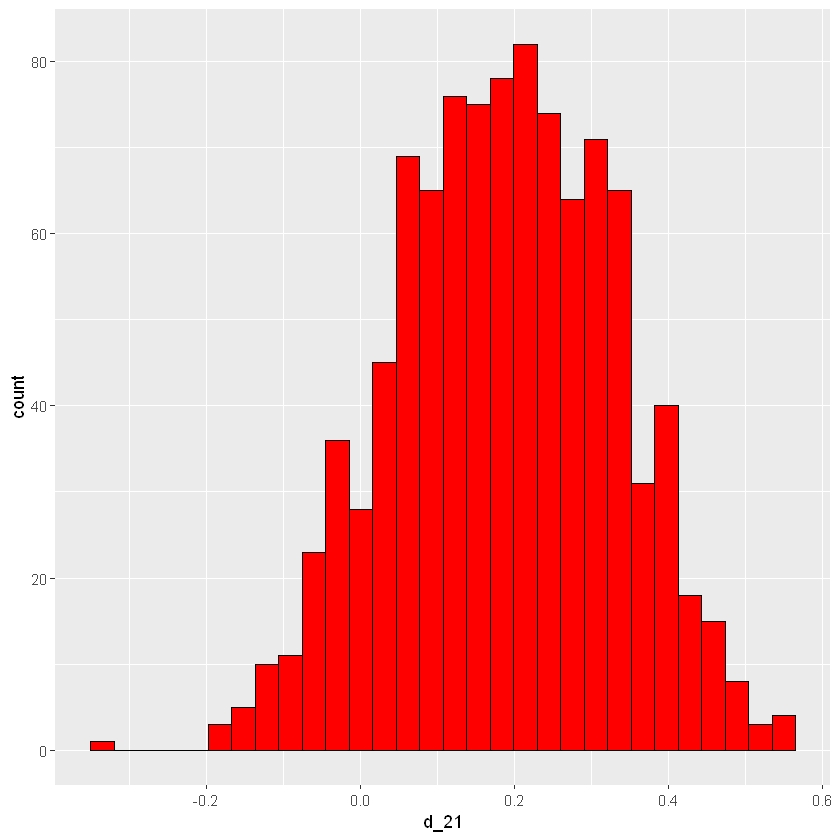
3
| # plot differenze
ggplot(df, aes(d_21)) +
geom_histogram(color="black", fill="red", bins=30)
|
1
2
| # intervallo di credibilità per d
quantile(df$d_21, c(0.05, 0.95))
|
5%:-0.0468267513603719; 95%:0.410351553897697
\(P(-0.05<p_M-p_W<0.41)=0.9\)
Dal momento che gli interavalli contengono lo zero, non c’è evidenza significativa per dire che le proporzioni sono differenti.
1
2
| # clear environment
rm(list=ls())
|
Normal model inference (\(\sigma\) sconosciuto)
Sia \(y\) una v.a. che modella i secondi necessari per calciare un rigore.
Prima abbiamo fatto inferenza su \(M\) campionando un modello normale, assumendo una deviazione standard \(S\), adesso entrambi parametri sono sconosciuti.
Sia \(M\) che \(S\) sono continue, usiamo una priori “non-informativa”.
\(g(M,S)=\frac{1}{S}\)
Verosimiglianza
1
2
3
4
5
6
| # observed data
df <- data.frame(Player="One",
Time_to_Serve = c(20.9, 17.8, 14.9, 12.0, 14.1,
22.8, 14.6, 15.3, 21.2, 20.7,
12.2, 16.2, 15.6, 19.4, 22.3,
14.1, 18.1, 23.6, 11.0, 17.3))
|
1
2
| # verosimiglianza
# Likelihood <- prod(dnorm(Time_to_Serve, mean=M, sd=S))
|
[TO DO] NON COMPRENDO L’UTILITÀ DELLA FORMULA PRECEDENTE
1
| # prod(dnorm(df$Time_to_Serve, mean=mean(df$Time_to_Serve), sd=sd(df$Time_to_Serve))) # ha senso?
|
1.92001903740555e-24
Distribuzione a posteriori (modello lineare)
\(Posteriori \propto Verosimiglianza \times \frac{1}{S}\)
Simulo \((M, S)\) dalla posteriori a 2 parametri.
Questo modello normale si può vedere come un modello lineare con solo l’intercetta.
[TO DO] DA CAPIRE LA RELAZIONE
1
2
3
| # lm intercetta
fit <- lm(Time_to_Serve~1, data=df)
summary(fit)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| Call:
lm(formula = Time_to_Serve ~ 1, data = df)
Residuals:
Min 1Q Median 3Q Max
-6.205 -2.730 -0.455 3.545 6.395
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 17.205 0.851 20.22 2.62e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.806 on 19 degrees of freedom
|
Similiamo da una a posteriori di \((M,S)\) usando una priori non informativa
1
2
| # simuliamo da questo modello bayesiano
sim_fit <- arm::sim(fit, n.sims=1000)
|
1
2
3
| # estraggo i vettori simulati di M e S
sim_M <- coef(sim_fit)
sim_S <- arm::sigma.hat(sim_fit)
|
1
2
| # distribuzione a posteriori congiunta di M e S
ggplot(data.frame(sim_M, sim_S), aes(sim_M, sim_S)) + geom_point()
|
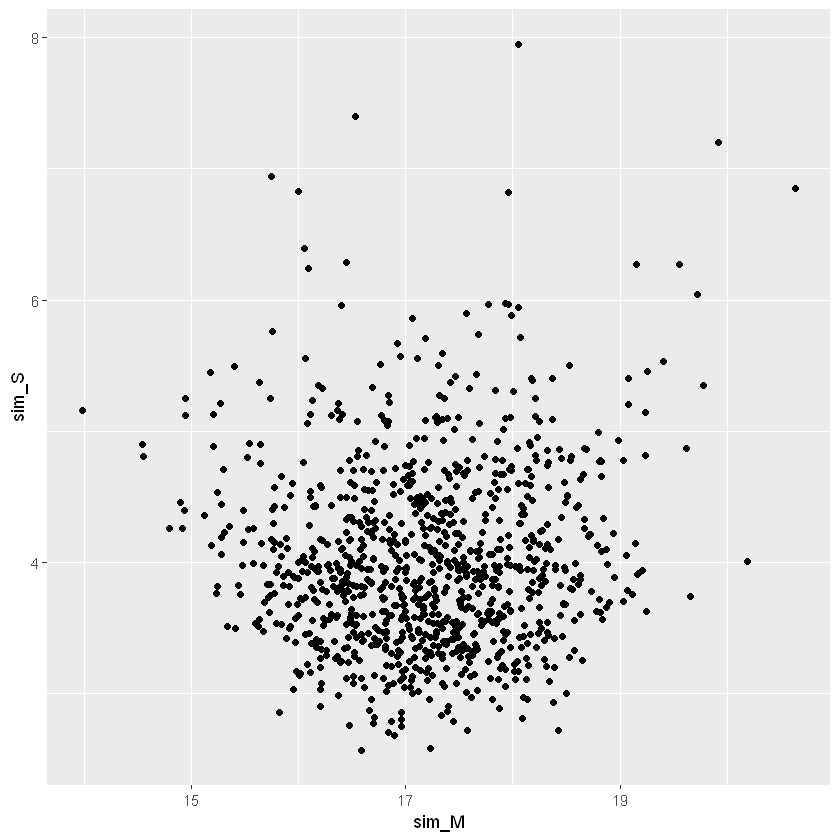
1
2
3
4
5
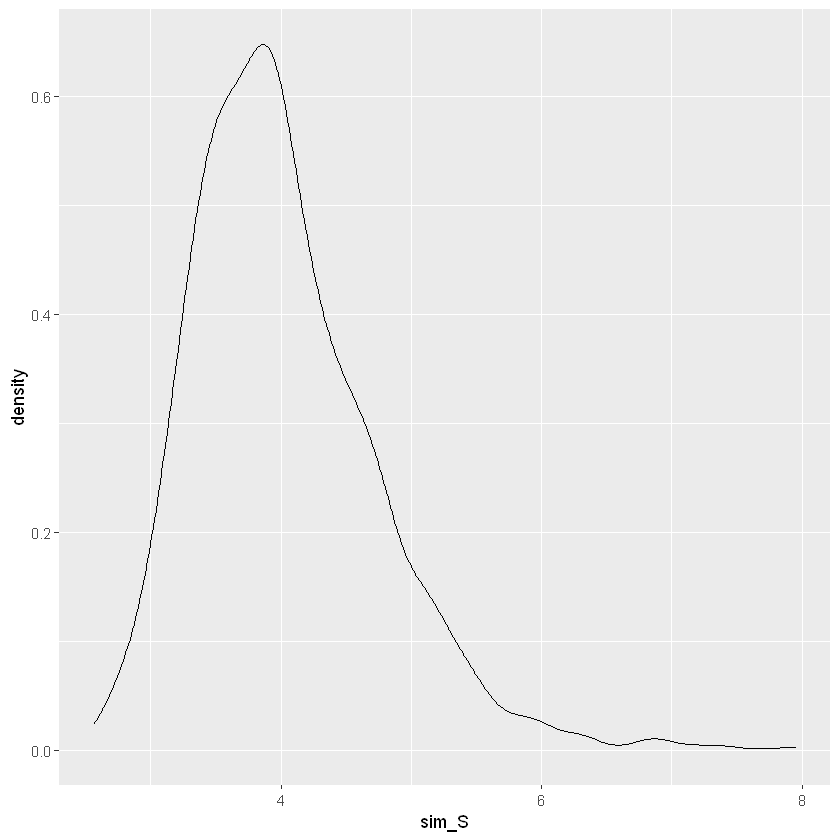
| # andamento deviazione standard
ggplot(data.frame(sim_S), aes(sim_S)) + geom_density()
# intervallo di crdeibilità al 90%
round(quantile(sim_S, c(0.05, 0.95)),3)
|
5%:3.093; 95%:5.313
Regressione Bayesiana
Sia \(y\) la variabile dipendente che rappresenta i secondi necessari per calciare un rigore.
Sia \(X\) la variabile indipendente che definisce il giocatore che calcia (Player One e Player Two).
Obiettivo: quanto è più lento il player 2 rispetto l’1?
Regression framework
\(y\sim\mathscr{N}\big(\beta_0+\beta_1\cdot I(\mbox{Player}=\mbox{Two}),S\big)\)
\((\beta_0,\beta_1,S)\sim\frac{1}{S}\)
Verosimiglianza
1
2
3
4
5
6
7
8
9
10
11
12
| # observed data
One <- data.frame(Player="One",
Time_to_Serve = c(20.9, 17.8, 14.9, 12.0, 14.1,
22.8, 14.6, 15.3, 21.2, 20.7,
12.2, 16.2, 15.6, 19.4, 22.3,
14.1, 18.1, 23.6, 11.0, 17.3))
Two <- data.frame(Player="Two",
Time_to_Serve = c(20.5, 25.1, 21.4, 25.6, 41.2,
23.9, 22.6, 19.0, 29.7, 36.4,
18.4, 20.3, 26.9, 28.9, 22.9,
31.5, 39.6, 29.4, 26.9, 24.5))
df <- rbind(One, Two)
|
1
2
| # verosimiglianza
# Likelihood <- prod(dnorm(Time_to_Serve, mean=beta0+beta1*I(Player2), sd=S))
|
[TO DO] NON COMPRENDO L’UTILITÀ DELLA FORMULA PRECEDENTE
Distribuzione a posteriori (modello lineare)
\(Posteriori\propto \mbox{Verosimiglianza}\times \frac{1}{S}\)
Questo modello normale si può vedere come un modello lineare.
[TO DO] DA CAPIRE LA RELAZIONE
1
2
3
| # stima del modello
fit <- lm(Time_to_Serve ~ Player, data=df)
fit
|
1
2
3
4
5
6
| Call:
lm(formula = Time_to_Serve ~ Player, data = df)
Coefficients:
(Intercept) PlayerTwo
17.20 9.53
|
In media il giocatore 1 impiega \(17.20\) secondi, mentre il giocatore 2 impiega \(17.20+9.53\) secondi.
1
2
3
4
| # generare dalla distribuzione a posteriori dei beta e sigma
sim_fit <- arm::sim(fit, n.sims=1000)
sim_beta <- coef(sim_fit)
sim_S <- arm::sigma.hat(sim_fit)
|
1
2
3
4
5
6
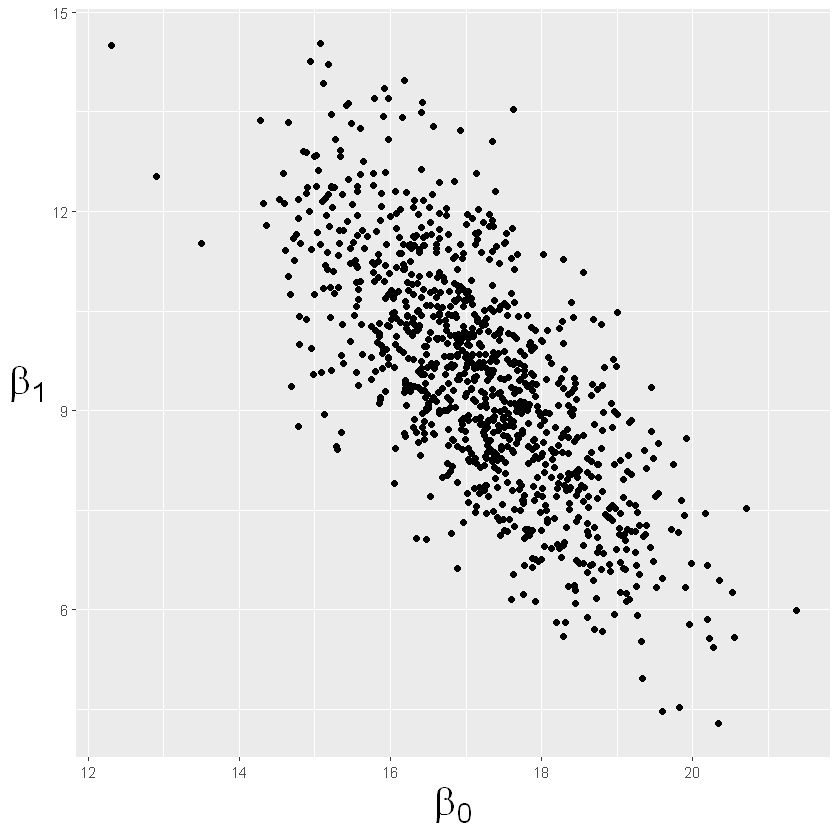
| # plot posteriori congiunta dei beta
sim_beta <- data.frame(sim_beta)
names(sim_beta)[1] <- "Intercetta"
ggplot(sim_beta, aes(Intercetta, PlayerTwo)) + geom_point() +
xlab(expression(beta[0])) + ylab(expression(beta[1])) +
theme(axis.title.y = element_text(angle = 0, vjust = 0.5), axis.title=element_text(size=24))
|
1
2
| # plot posteriori marginale di beta1
ggplot(sim_beta, aes(PlayerTwo)) + geom_density()
|
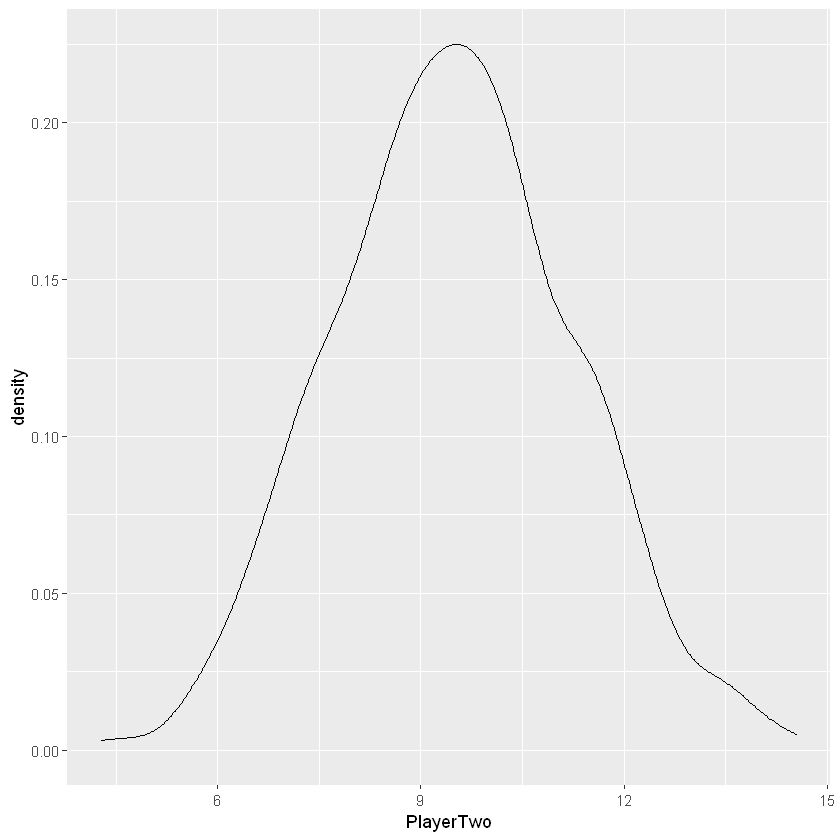
Il confronto diretto delle due distribuzioni marginali non è sensato, perché viene influenzato dalla differente variabilità delle due stime, quindi, è necessario standardizzarlo.
Standardized effect
\(h(\beta_1,S)=\frac{\beta_1}{S}\)
con \(\beta_1\) parametro di regressione e \(S\) deviazione standard.
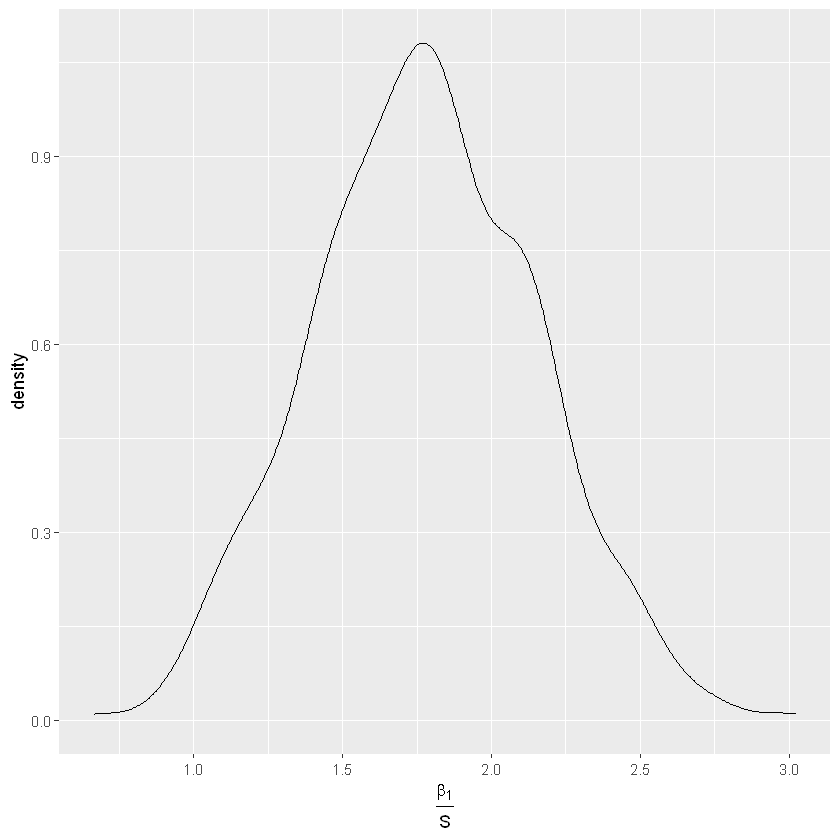
Effetto standardizzato: il tempo medio che il giocatore due è più lento del giocatore uno, misurato in unità di deviazioni standard.
1
2
3
4
5
| # plot posteriori marginale di beta1 standardizzato
posterior <- data.frame(sim_beta, sim_S)
standardized_effect <- with(posterior, PlayerTwo / sim_S)
ggplot(posterior, aes(standardized_effect)) + geom_density() +
xlab(expression(frac(beta[1],S)))
|
1
2
3
| # intervallo di credibilità al 90% per l'effetto standardizzato
round(quantile(data.frame(sim_beta)$PlayerTwo / sim_S, c(0.05, 0.95)),3)
|
5%:1.151; 95%:2.423
La probabilità che l’effetto standardizzato di \(\beta_1\) sia tra 1.2 e 2.4 è il 90%