Statistics: Event History Analysis

La presente pagina è ricca di errori e si sconsiglia il suo utilizzo.
Se vuoi suggerire qualche modifica, puoi semplicemente proporla da GitHub

Metodi per l’analisi di dati di durata

Basi dell’analisi dei dati di durata

Concetti base

Ambiti ed esempi

Definizioni base

• Dominio (es variabile qualitativa d’interesse) e spazio degli stati (modalità della variabile qualitativa)
• Evento: failure, comporta una transizione dello stato
• Episodio: episode, spell length, survival time, duration, il tempo tra l’esposizione al rischio e il failure
• Evento origine: evento che porta l’esposizione al rischio
• Popolazione a rischio

Processi

• Caso semplice: 1 episodio, 1 stato destinazione
• Multistato o rischi competitivi: 1 episodio, 2+ stati destinazione
• Multi-episodio: 2+ episodi, 1 stato destinazione
• Multistato e multi-episodio

Limiti modello lineare

Il tempo è sempre positivo, non è normale e sono presenti le censure, inoltre le esplicative possono essere tempo dipendenti (cambiano stato durante l’episodio).

Censure

Scegliere sono episodi non censurati comporta dei bias di selezione. Il tempo dell’episodio si caratterizza da una variabile dummy che definisce la eventuale censura.

Censure in ambito bio-statistico

• a destra: l’evento avviene dopo la fine del periodo di osservazione
• a sinistra: l’evento avviene prima dell’inizio del periodo di osservazione

Censure in ambito sociale

• a destra: l’evento avviene dopo la fine del periodo di osservazione
• a sinistra: l’evento origine avviene prima dell’inizio del periodo di osservazione

Tipi di censure

• Tipo I (generati dalla fine del periodo di analisi)
• Tipo II (osservazione termina dopo che si è verificato un certo numero di eventi)
• Random-non informative (non dipendono dal rischio)
• Random-informative (dipendono dal rischio, sono problematiche)

Disegni di indagine

Trasversali

Rilevano stati in un preciso istante di tempo. Esempi: censimento ISTAT

Longitudinali prospettivi

Rilevano stati nel corso del tempo.

Panel puro o con ricostruzione retrospettiva (tra waves)
Pro: non si perdono individui per emigrazioni, no problemi di memoria, consente la rilevazione di dati non fattuali (opinioni).
Contro: costi, troncamento a sinistra (puro), difficile per fenomeni rari o emergenti, possibili incoerenze tra waves, rischio selezione (attrito), re-test effect (ridondanza di risposte).
Esempi: EU-SILC panel puro; SHARE panel con retrospettiva.

Studi di follow-up
Sono panel molto lunghi, si seguono specifiche coorti e si ricostruiscono gli eventi più importanti tra i follow-up.
Pro: tempi di osservazioni lunghi, valutazioni degli effetti a lungo termine, legami intergenerazionali.
Contro: attrito, costi, vuoti informativi, tempi di sopravvivenza troncati (non si supera una certa età).
Esempi: Millennium Cohort Study UK; National Longitudinal Survey USA; paesi nord europei.

Record-Linkage
collegano informazioni di eventi e/o stati da fonti amministrative o statistiche. Linkage deterministico o probabilistico.
Esempi: Linkage danese; analisi ISTAT; tradizione nordica

Longitudinali retrospettivi

Si rilevano cross-section ma si ricostruisce la storia degli stati avvenuti in passato (es. Famiglie e Soggetti Sociali FSS ISTAT; Gender & Generation Survey).
Pro: ricostruzione tratti lunghi, bassi costi, rilevazione continua, tempi brevi.
Contro: memoria, selezione, non adatto per dati non fattuali.
La data dell’intervista serve per ricostruire la durata degli episodi censurati: se non c’è l’evento (si ha quindi censura), la differenza tra l’intervista e l’evento di origine definisce la durata dell’episodio, se non è censurato è la differenza tra l’intervista e la data dell’evento.

Funzioni base nel continuo e nel discreto

Funzioni base con tempo continuo

• Condizioni
• Densità, Ripartizione, Sopravvivenza
  \(S(t)=1-F(t)=1-\int_0^t f(t)dt=\int_t^{\infty} f(t) dt\)
  La distribuzione di \(T\) è impropria o difettosa in quanto la sopravvivenza può non raggiungere 0. \(S(+\infty)=g\) con \(g\) probabilità di essere immune all’evento (‘long-term survivors’)
• Funzione di rischio Hazard (propensione al cambiamento)
  \(h(t)=\lim_{t'\rightarrow t}\frac{\mathbb{P}(t\le T \le t' \vert T \ge t)}{t'-t}\equiv\frac{f(t)}{S(t)}\)
  Come la densità, non è una probabilità ma lo è se si moltiplica il suo valore per l’intervallo di tempo in cui la si stima.
• Rischio integrato (utile per informazioni sul rischio quando non si può determinare)
  \(H(t)=\int_0^t h(t)dt=-\log{S(t)}\)
• Relazioni tra le funzioni

Funzioni base con tempo discreto

• Discreto
• Continuo discretizzato

Probabilità nel punto \(\mathbb{P}(T=t_i)=f(t_i)\)
Sopravvivenza \(\mathbb{P}(T\ge t_i )=\sum f_s\)
Hazard \(\mathbb{P}(T\ge t_i \vert T \ge t_i)=f(t_i)/S_i\)

Tipologie di metodi

Metodi non parametrici e modelli di regressione.
I modelli di regressione possono essere parametrici (assumendo forma della baseline e del link tra covariate e baseline - tutti i modelli AFT) o semiparametrici (assumendo solo il link tra covariate e baseline - solo modelli di Cox)

Metodi per tempo continuo

• Metodi non parametrici: Kaplan-Meier (Product-Limit)
• Modelli di regressione (le covariate influenzano):
  • Rischi proporzionali PH \(h(t)=h_0(t) \cdot \exp{(\beta X)}\)
  • Tempi accelerati AFT \(T=T_0 \cdot \exp{(\beta X)}\)

Metodi per tempo discreto

• Metodi non parametrici: Life Table (Actuarial Method)
• Modelli di regressione: Logit, Probit

Metodi non parametrici

Kaplan-Meier (Product Limit)

• Calcolo delle funzioni e indici
  1. Siano \(n=6\) episodi di durata \((4,3*,6,6*,10,18)\)
  2. Rappresento sull’asse T gli episodi nel seguente modo
     
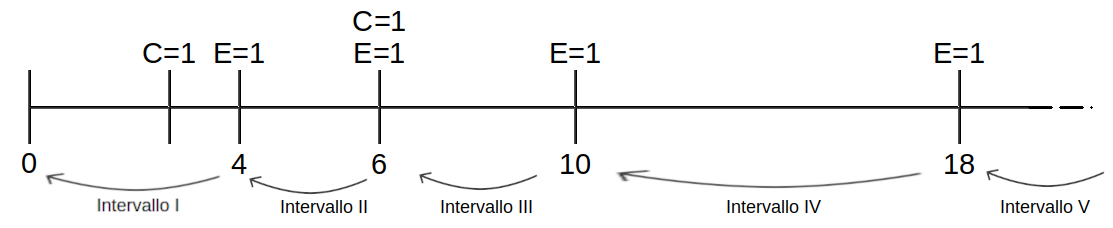
  3. Siano:
     • \(R_j=N-\sum_{k=1}^{j-1}(C+E)_k\) i soggetti a rischio di sperimentare l’evento in quel punto
     • \(\hat{q}_j=\frac{E_j}{R_j}\) la probabilità di sperimentare l’evento
     • \(\hat{p}_j=1-\hat{q}_j\) probabilità di non sperimentare l’evento
     • \(\hat{S}_j=\prod_{k=1}^{j-1}\hat{p}_k\) la sopravvivenza nel punto
  4. Si calcola quanto segue
     
  5. Si sintetizzano le informazioni
     
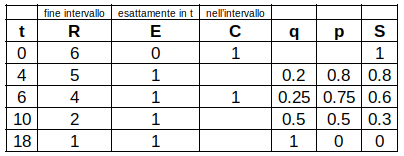
  6. Si rappresenta la sopravvivenza
• Metodi per la stima del rischio integrato (le stime dirette sono errate, come \(f\), perché dipendono dalla variabilità delle ampiezze degli intervalli e il numero di eventi in ogni intervallo è teoricamente sempre 1)
  1. \(\hat{H}(t)=\hat{H}_j=-\log{\hat{S}_j}\) (prima si stima \(S_{\small{\mbox{KM}}}\) e poi \(H\))
  2. Stimatore Nelson-Aalen: somma di prodotti tra stime del rischio in punti medi (si può stimare anche \(S_{\small{\mbox{NA}}}\) e solitamente è sovrastimata)
• Esplorazione forma del rischio: esame grafico di \(H\) se cresce linearmente \(h\) è costante, oppure differenziando numericamente \(H(t)\) previa lisciatura

Pro: la stima \(S\) è MV; non è influenzato dalla scelta degli intervalli; usa tutta l’informazione
Contro: difficile da tabulare con molti episodi; non utilizzabile se il tempo non è misurato esatto; non consente stima diretta del rischio

Life Table (o Attuariale)

• Tavola di eliminazione: stima rischio, probabilità e sopravvivenza
  \(N_j=N_{j-1}-(E_{j-1}+C_{j-1})\)
  \(R_j=N_{j}-0.5\cdot C_j\)
  \(\hat{p}_j=1-\frac{E_j}{R_j}\)
  \(\hat{S}_j^*=\hat{p}_{j-1}\cdot S_{j-1}\)
• Altre funzioni
  Formula di Greenwood \(\mbox{SE}(\hat{S}_j)\approx \hat{S}_j^* \cdot \left [ \sum_{k=1}^{j-1} \frac{\hat{q}_k}{(1-\hat{q}_k)R_k} \right ]^{1/2}\)
  Sopravvivenza nell’intervallo \(\overset{\approx}{S}(t)=\hat{S}_j+(\hat{S}_{j+1}-\hat{S}_j)\frac{t-t_j}{t_{j+1}-t_j}\)
  Sopravvivenza a metà intervallo \(\bar{S}_j=0.5\cdot (S_j+S_{j+1})\)
  Ripartizione \(\hat{F}_j=1-\hat{S}_j\)
  Densità di probabilità \(\hat{f}_j=\frac{\hat{F}_{j+1}-\hat{F}_j}{t_{j+1}-t_j}=\frac{S_{j+1}-S_j}{t_{j+1}-t_j}\)
  Standard Error approssimato \(\mbox{SE}(\hat{f}_j)\approx \frac{\hat{q}_j\hat{S}_j}{t_{j+1}-t_j}\cdot \left [ \sum_{s=1}^{j-1} \frac{\hat{q}_s}{(1-\hat{q}_s)R_s} + \frac{(1-\hat{q}_s))}{\hat{q}_sR_s} \right ]^{1/2}\)
  Tasso di transizione \(\hat{h}_j=\frac{\hat{f}_j}{\overset{\approx}{S}_j}\) non costante all’interno dell’intervallo (diversamente dalla densità)
  Standard Error approssimato \(\mbox{SE}(\hat{h}_j)\approx \frac{\hat{h}_j}{\sqrt{\hat{q}_j\hat{R}_j}} \cdot \sqrt{1-\left ( \frac{\hat{h}_j(t_{j+1}-t_j)}{2} \right )^2}\)
  Tasso di transizione a metà intervallo \(\bar{h}_j=\frac{\hat{f}_j}{\bar{S}_j}\)
  Intervallo di sopravvivenza \(\hat{S}(t)\pm z_{\frac{\alpha}{2}} \cdot \mbox{SE}(\hat{S}(t))\)
• Esplorazione forma del rischio: esame grafico di \(H\) se cresce linearmente \(h\) è costante, oppure differenziando numericamente \(H(t)\) previa lisciatura

Pro: semplice; veloce; consente la stima anche con tempo impreciso; stima diretta di \(h(t)\) e \(f(t)\)
Contro: l’ampiezza degli intervalli è soggettiva, non adatto per piccoli campioni; approssimare ad un intervallo significa non usare tutta l’informazione disponibile

Confronti e omogeneità

Per analizzare le differenze tra funzioni di sopravvivenza appartenenti a gruppi differenti si possono confrontare i quantili, le funzioni di sopravvivenza mediante i grafici (se gli intervalli di sopravvivenza si sovrappongono) o effettuare test di omogeneità.

I test di omogeneità saggiano se le distribuzioni degli episodi tra i gruppi sono significativamente diverse.
I dati censurati non consentono metodi standard come il Kruskal-Wallis, in questo contesto si utilizzano test simili al chi quadro

• Log-rank test (Mantel-Cox; generalized savage test): somma quadratica degli scarti tra il numero di eventi nel gruppo e il suo corrispettivo valore atteso (ipotesi distribuzione delle durate uguale per tutti) diviso la varianza dello scarto. Più utile per i punti finali della curva.
• Wilcoxon test (Wilcoxon Breslow Gehan), come il Log-rank ma pesa le differenze tra gli scarti con il numero di individui a rischio. Più utile per i punti iniziali della curva.
• Tarone-Ware
• Peto-Prentice

Rischi competitivi

Quando si ha un episodio e più stati di destinazione, si può stimare la pseudo-sopravvivenza.
La procedura è gestibile sia con stime KM che LT.
Come nel caso della transizione singola, ma gli episodi che non terminano nella destinazione k-esima si trattano come censurati (se vale l’ipotesi di indipendenza).
Ipotesi di indipendenza: l’eliminazione di un rischio non modifica la sopravvivenza rispetto agli altri.

Modelli a tempo continuo

Modelli semi-parametrici

Se il numero di gruppi aumenta e la dimensione campionaria è piccola, l’approccio parametrico non è adeguato e si usano i modelli di regressione.

Modello di Cox

Si vuole stimare la propensione per i soggetti di sperimentare un certo evento.
Il rischio è dato dal rischio base (non parametrico) con tutte covariate nulle e un fattore (parametrico) legato alle covariate
\(h_i(t,X)=h_0(t)\cdot \exp{(\beta x_i)}\)

Per covariate continue, alla variazione unitaria della variabile d’interesse, il logaritmo del rischio varia di \(\beta\).
Per covariate dicotomiche, il cambio di classe fa variare il logaritmo del rischio di \(\beta\) rispetto la classe base.
Proportional Hazard: il rapporto tra i rischi di due individui con differenti covariate è costante nel tempo.

Pro: robusto (i coefficienti approssimano bene in modo parametrico); con poche assunzioni fornisce informazioni sulla sopravvivenza; flessibile (estensioni tempo dipendenti e con effetti non proporzionali); non richiede una stima del rischio di base.

Si sceglie la baseline soggettivamente per dare senso all’interpretazione.

Significatività

Per valutare se i parametri sono significativamente diversi da 0, si usa la statistica di Wald (chi-quadro o z).
Gli intervalli di confidenza
coefficienti: \(\beta=\pm 1.96 \cdot \mbox{SE}(\beta)\)
hazard ratio: \(\exp{\beta}\)

Risk Score

Dato \(i\)-esimo individuo con \(X_1,...,X_k\) caratteristiche, il risk score risulta
\(\mbox{RS}=\exp{\left ( \sum_{i=1}^k \beta_i X_i \right ) }\)
è una misura relativa rispetto la baseline ed è utile quando si stimano modelli con numerosi predittori.
Rischio Relativo \(\exp{\beta_i}\) di una variabile dummy \(X_1\)

Bontà di adattamento

Per modelli nidificati: test rapporto di verosimiglianza (verosimiglianza parziale) LR che saggia l’ipotesi nulla tutte le covariate nulle
\(\mbox{LR}=-2\log{L_{\small{Reduced}}} - (-2\log{L_{\small{Unreduced}}})\sim \mathcal{X}^2_g\)
\(g=p_{\small{Unreduced}}-p_{\small{Reduced}}\) con \(p\) numero di parametri

Per modelli non nidificati: AIC, BIC

Stima di massima verosimiglianza

Full Likelihood - “Qual è la probabilità che l’individuo i-mo sperimenti un evento nel \(t_j\) osservato?’’
la verosimiglianza in situazioni di censura si decompone nel seguente modo
\(L(\alpha, t_1,...,t_N)=\prod_{i\in E} f(t_i,\alpha) \cdot \prod_{i\in C} S(t_i,\alpha)=\prod_{i\in E} h(t_i,\alpha) \cdot \prod_{i\in N} S(t_i,\alpha)\)
con \(\alpha\) parametro generico, \(E=N-C\) casi non censurati, \(C\) casi censurati, \(f=S\cdot h\)
successivamente si applica il logaritmo e si massimizza rispetto \(\alpha\), ma il rischio di base non è specificato (non si conosce a distribuzione dei tempi di sopravvivenza e non si può trovare un unico set di parametri che massimizza la verosimiglianza). Soluzione: Partial Likelihood.

Partial Likelihood - “Dato che qualcuno sperimenta un evento al tempo \(t_j\) qual è la probabilità che si tratti dell’individuo i-mo?’’
Si ordinano tutti i tempi (censurati e non) in modo crescente e si calcola il contributo al rischio di ciascun soggetto alla PL (\(t^*_{ij}\) probabilità condizionata che l’unità \(i\) sperimenti l’evento al tempo \(t_j\)).
\(\mbox{PL}=\prod_E \frac{h(t^*_{ij})}{\sum_R h(t^*_{ij})}\)
con \(R\) insieme a rischio di eventi avvenuti al tempo \(t^*_{ij}\) e successivi (sia censurati che no, ma il numeratore è solo per gli eventi).
Divido num. e den. per rischio di base, ne faccio la trasformata logaritmica e massimizzo con metodi numerici iterativi.

Pro: stime PML asintoticamente normali e non distorte.

Note: sulla stima FL entrano tutti i casi, mentre nella PL solo al denominatore i censurati. Basato sui rank dei tempi non sono rilevanti i tempi ma l’ordinamento e l’aggiunta di una costante (parte non parametrica) non influisce sulle stime dei parametri.

Ties

Il metodo PL assume che non ci sono episodi coincidenti, bisogna correggere la PL.

• Exact (tutti i possibili ordinamenti)
• Breslow (come Exact ma shrinkage to 0 se ci sono molti ties)
• Efron (come Breslow ma più vicino all’Exact)
• Discrete (eventi effettivamente doppioni)

Stima e utilizzo delle funzioni base

Il modello di Cox stima i rischi relativi, e non consente di capire l’entità del rischio in termini assoluti, in quanto non si ha una stima del rischio di base \(H_0(t)\).
Senza variabili tempo dipendenti, si può stimare il rischio di base con metodi non parametrici (es. KM, Nelson-Aelen), oppure usando le seguenti relazioni
\(S(t,X)=S_0(t)^{\exp{\left ( \sum_{i=1}^k \beta_i X_i \right ) }}\)
con \(S_0\) non parametrico, la parte esponenziale (risk score) stimata con Cox e si possono combinare le componenti per stimare la funzione di sopravvivenza per qualsiasi gruppo diverso dal base.
\(H(t,X)=H_0(t) \cdot \exp{\left ( \sum_{i=1}^k \beta_i X_i \right ) }\)
Inoltre, \(S(t,X)=\exp{(-H(t,X))}\) quindi si può stimare dall’una l’altra

Variabili tempo-dipendenti

• Processi: micro (dettagli su individui), meso (vite, gruppi piccoli), intermedio (contesti aziendali), macro (processi storici)
• Caratteristiche VTD
• Modello con VTD (esempio con due covariate di cui una tempo dipendente)
  \(h_i(t,X)=h_0(t)\cdot \exp{(\beta_1 X_{i1}+\beta_2 X_{i2}(t))}\)
• Episode splitting per tenere sotto controllo le VTD:
  1. Trasformazione della tabella dati in person-period (si splittano gli gli episodi con variazione della VTD in sotto episodi censurati e non): le unità con un cambiamento della esplicativa al tempo \(t_1\) dentro l’episodio \([t_0,t_2]\), si splittano in due eventi, il primo censurato di lunghezza \(t_1-t_0\), il secondo \(t_2-t_1\) con l’evento (censurato o no), con le altre covariate fisse.
  2. Applicazione dei modelli di durata alla nuova tabella dati
• Spazio stati TD
  • Dicotomizzazione non reversibile
  • Dicotomizzazione reversibile (stati ricorrenti)
  • Strutture complesse
• Effetti immediati o differiti nel tempo
  • Contestuale (l’evento dipende dal valore covariata al tempo \(t\) precedente
  • Differito ‘lag-time effect’ (l’evento dipende dal valore covariata in un tempo \(t^*=(t-L)\)

Effetti non proporzionali

• Violazione assunzione proporzionalità
• Verifica proporzionalità
  • Analisi grafica del logaritmo del rischio cumulato (se non sono parallele)
    \(\log{(H)}=\log{(-\log{(S)})}\)
    Se il rapporto tra i rischi di due soggetti è costante (PH), anche la differenza tra \(\log{H}\) dei due soggetti differisce per una costante al variare di \(t\)
  • Residui di Schoenfeld (se l’andamento dello scarto tra la covariata dell’i-esimo individuo e la sua media nel tempo non è casuale)
  • Modello con interazione tra tempo e covariate (se il coeff. dell’interazione è significativamente diverso da zero)
    \(h_i(t,X)=h_0(t) \cdot \exp{(\beta_1 X_i + \beta_2 X_i \cdot g(t))}\)
• Superamento ipotesi proporzionalità
  • Modello stratificato (\(n\) rischi di base quanti gli strati)
    \(h_{ig}(t,X)=H_{0g}(t) \cdot \exp{\left ( \sum_{i=1}^k \beta_i X_i \right ) }\)
  • Modelli separati in strati (\(n\) modelli quanti gli strati, con \(\mathcal{X}^2\) saggio se gli \(n\) modelli sono uguali a quello compatto)
    \(\mathcal{X}^2_{(k-1)p}=\bigg[-2LL_{\mbox{stra}}-\Big[\sum_{i=1}^n(-2LL_{\mbox{sep}_i})\Big]\bigg]\)
    con \(k=\mbox{n.strati}\) e \(p=\mbox{n.predittori}\)
  • Modello con interazione tra il tempo e le covariate (non solo per valutare la proporzionalità ma anche per superarla). Bisogna scegliere \(g(t)\)
    • Tempo continuo
      • Effetto lineare
      • Effetto lineare traslato
      • Effetto logaritmico (il parametro rappresenta la variazione del log rischio a raddoppi della durata, se il logaritmo è in base 2; pro-tip incrementare di 1 il tempo evita valori negativi)
    • Tempo discreto
      • Main effect: effetto principale (variabile senza dummy) + parte lineare con dummy (della stessa variabile) dell’intervallo (consente di capire se un tratto è significativamente diverso dall’altro)
      • Effetto a gradini: lineare con \(k\) dummy pari al numero di intervalli senza effetto principale (l’effetto potrebbe essere significativamente diverso da quello di base ma non è strettamente non proporzionale perché non è detto che i coefficienti che si stimano siano significativamente diversi da quelli stimati nel tratto precedente)

Modelli parametrici

Calcolo delle funzioni di densità, sopravvivenza e rischio

• Trasformazioni utili:
  \(\log{X}\sim\mathcal{N}(\mu,\sigma^2)\Rightarrow X\sim\log{\mathcal{N}(\mu,\sigma^2)}\)
  \(S(t)=\mbox{Pr}\{T\ge t\}=1-F(t)=\int_t^{+\infty}f(x)dx=\exp{\Big\{-\int_0^t h(x)dx\Big\}}\)
  \(h(t)=\frac{-d[S(t)]}{dt}/S(t)=\frac{f(t)}{S(t)}=-\frac{d}{dt}\log{S(t)}\)
  \(H(t)=\int_0^t h(x)dx\)
  \(\mu=\int_0^\infty S(t)d(t)\)
• Possibili forme funzionali:
  • Esponenziale
    \(f(t)=a\cdot \exp{(-at)}\mbox{ con }a>0\)
    \(S(t)=\exp{(-at)}=\exp{\big\{-H(t)\big\}}\)
    \(h(t)=a\) Rischio costante, memorylessness distribution
    \(H(t)=-\log{S(t)}=at\) (area sottostante ‘\(a\)’ fino a \(t\))
    Test grafico su Esponenziale: se l’andamento \(H(t)\) vs \(t\) è una linea retta che parte dall’origine allora i dati approssimano bene una durata esponenziale (quindi Weibull con \(b=1\)).
    \(F(t)=1-\exp{(-at)}\)
    \(\log{S(t)}=-at\)
  • Weibull
    \(f(t)=abt^{b-1}\exp{(-at^b)}\) con
    \(a\) (livello o scala), \(b>0\) (forma), se \(b=1\) Exp (test \(H_0:b=1\rightarrow\mathcal{X}^2_1\))
    \(S(t)=\exp{(-at^b)}\)
    \(h(t)=abt^{b-1}\) Rischio costante se \(b=1\), monotono crescente se \(b>1\), monotono decrescente se \(b<{1}\)
    \(H(t)=-\log{S(t)}=at^b\)
    Test grafico su Weibull: se l’andamento \(\log{H(t)}\) vs \(\log{t}\) è una retta con intercetta \(\log{a}\) e pendenza \(b\)
  • Gompertz e Gompertz-Makeham (utile per mortalità con pochi casi)
    \(h(t)\) Rischio monotono
  • Log-logistica
    \(h(t)\) Rischio monotono decrescente o unimodale
  • Hernes, Sickle, Coale-McNeil
    \(h(t)\) Rischio unimodale
  • Altre: Log-normale, Gamma, Gamma generalizzati

Modelli di regressione parametrici

• Parametrizzazione a Rischi Proporzionali (PH)
  • La variabile dipendente è la funzione rischio (come Cox ma con baseline parametrico):
    \(h_i(t,X_i)=h_0(t)\cdot \theta\)
  • Trasformazioni utili
    \(S(t)=S_0(t)^\theta\)
    \(f(t)=f_0(t)\cdot S_0(t)^{(\theta-1)}\cdot\theta\)
    \(H(t)=H_0(t)\cdot\theta\quad\mbox{ con }H_0(t)=-\log{S_0(t)}\)
• Parametrizzazione a Tempi Accelarati (AFT)
  • Si ha un effetto moltiplicativo, non più sul rischio, ma sul tempo di permanenza nello stato pre-transizione:
    \(T_i=T_0\cdot \gamma\) con \(\gamma\) fattore di accelerazione, e se è \(>1\) aumentano i tempi di sopravvivenza e il rischio diminuisce
  • Trasformazioni utili
    \(S(t,X)=S_0\big(\frac{t}{\gamma}\big)\)
    \(h(t,X)=h_0\big(\frac{t}{\gamma}\big)/\gamma\)
    \(f(t,X)=h_0\big(\frac{t}{\gamma}\big)/\gamma\cdot S_0\big(\frac{t}{\gamma}\big)=f_0(t)/\gamma\)
• Specifiche parametrizzazioni per specifici modelli
  • Weibul (Esponenziale): sia PH che AFT
  • Gompertz: PH
  • Log-normale, Log-logistico, Gamma generalizzati: AFT

Parametr. PH e AFT per i modelli Esponenziale, Weibull ed Esponenziale a tratti

• Esponenziale
  • Funzioni utili
    \(T\sim\mathcal{Exp}(a)\sim\mathcal{W}(a,\sigma =1)\)
    \(lim_{t\rightarrow\infty}S(t,a)=0\) eventi inevitabili
    \(E(T)=\frac{1}{a} \qquad Var(T)=\frac{1}{a^2}\)
    \(t_{\mbox{quantile}_q}=-\log{(q)}\cdot E(T)\) (es. mediana \(t_{ME}=0.693/a\))
    \(h(t,a_k)=a_k\) se 1 episodio, più destinazioni (rischi competitivi), con \(a_k\) tasso di transizione (costante) verso destinazione \(k\)
  • PH (stimo il rischio assoluto)
    \(h(t,X)=\exp{\beta_0}\cdot\exp{(\beta X)}=h_0\cdot\exp{(\beta X)}\)
    Si noti che $\exp{(\beta X)}$ è il Rischio Relativo nel caso di \(X=1\) (dummy)
    Rispetto i modelli di Cox: \(h_0\) è parametrico e il rischio non dipende dal tempo
    Per leggerli in ottica di durata media: \(E(T\vert X=k)=\frac{1}{h(t\vert X=k)}\)
  • AFT (stimo la durata media)
    \(T=\big[\exp{(\alpha_0)}\cdot\exp{(\epsilon)}\big]\cdot\exp{(\alpha X)}=T_0\cdot\gamma\)
    Si dimostra che per l’esponenziale \(\alpha=-\beta\)
    L’exp dei singoli coefficienti è il tempo relativo.
    \(\alpha\) stimato è il logaritmo della durata relativo alla variabile \(X\)
    \(\exp{(\alpha_0^{AFT})}=\exp{(-\beta_0^{PH})}=1/\exp{(\beta_0^{PH})}=1/h_0^{PH}=E(T_0)\)
    \(\hat{a}_{\small{\mbox{MV}}}=\frac{E}{\sum_{i\in N}t_i}=\) rapporto tra numero di eventi (casi non censurati) e totale dei tempi \(t_i\) dell’intero campione (sia censurati che non)
    \(\hat{E}(t)=\frac{1}{\hat{a}_{\small{\mbox{MV}}}}=\) durata media intervallo
• Weibull
  • PH
    \(h(t\vert X)=\big[\exp{(\beta_0)}\cdot bt^{b-1}\big]\cdot\exp{(\beta X)}=h_0(t)\cdot\exp{(\beta X)}\)
  • AFT
    \(\log{T}=\alpha_0+\alpha X+\sigma\epsilon\)
    \(T=\exp{(\alpha_0+\sigma\epsilon)}\cdot\exp{(\alpha X)}=T_0\cdot\gamma\)
    Si dimostra che \(\beta=\beta_{PH}=-\beta_{AFT}\cdot b=-\alpha\cdot b\)
    NB. SAS stima modello Weibull solo AFT con \(\sigma=1/b\Rightarrow\beta_{PH}=-\beta_{AFT}\cdot (1/\sigma)\)
    Inoltre, con \(a=\exp{(-\beta_{AFT}\cdot b)}\) si ricava facilmente \(h(t)=\exp{(-\beta_{AFT}\cdot 1/\sigma)}\cdot 1/\sigma\cdot t^{(1/\sigma -1)}\), così da ottenere il rischio dopo \(t\) durate
    \(\alpha=(1/\sigma -1)\) incremento di rischio all’aumento dello \(0.01\) del tempo.
• Esponenziale a tratti (Piecewise exponential model)
  Per \(L\) sotto-intervalli del tempo si specificano diverse distribuzioni parametriche del rischio.
  • Funzioni utili
    \(h(t_j)=\sum_j^L a_j I_j\) con $I_j$ variabile dummy che vale \(1\) nel $j-$esimo intervallo. Rischio costante a tratti, con valori di \(a\) differenti per ogni intervallo.
    \(h(t_j,X)=a_j=\exp{(\beta_{0j}+\beta_j X)}\mbox{ con }j=1,...,L\) è un modello a rischi non proporzionali, varia ad ogni intervallo. Se \(\beta_j=\beta\) è a rischi proporzionali.
    NB. in SAS la significatività di J è con Wald, in cui si saggia se il rischio è costante
    NB. in SAS exp(-coeff.) è il valore del rischio relativo rispetto al \(j-\)esimo tratto

Modelli Frailty

Frailty models o Mixed Proportional Hazard models (misti si intende con effetti fissi e casuali).

Introduzione al concetto di Frailty

Problema

Limitare il problema della mal specificazione del modello e distorsione delle stime, aggiungendo un effetto casuale sui modelli di regressione sul rischio.
Anche con covariate indipendenti tra loro, se una delle due è omesse andrà ad impattare le stime selezionando la popolazione e rendendo le stime dipendenti dal tempo (rischio ad U, individui fragili escono prima e si selezionano i più resistenti nel tempo).
La presenza di una fragilità differente tra i gruppi - eterogeneità non osservata - comporta una variazione del rischio; i modelli tradizionali di Survival Analysis considerano le popolazioni omogenee, cioè che tutti gli individui hanno lo stesso rischio.

• Funzione di sopravvivenza marginale per due popolazioni esponenziali \((\lambda_i)\)
  \(S(t)=p\exp{(-\lambda_1 t)}+(1-p)\exp{(-\lambda_2 t)}\) è una mistura e se si calcola il rischio (derivando \(\log{S}\)) non è più costante.
• Funzione di rischio marginale per due popolazioni esponenziali
  \(h(t)=-\frac{\partial \log{S(t)}}{\partial t}=\frac{p\lambda_1\exp{(-\lambda_1 t)}+(1-p)\lambda_2\exp{(-\lambda_2 t)}}{p\exp{(-\lambda_1 t)}+(1-p)\exp{(-\lambda_2 t)}}\)

Modello Frailty

Sia \(U>0\) v.a. indipendente dal tempo, la cui varianza \(\sigma^2_U\) misura l’eterogeneità non osservata della popolazione. Siano \(\mathbf{X}=(X_1,...,X_k)\) matrice delle covariate e \(\mathbf{\beta}=(\beta_1,...,\beta_k)\) parametri di regressione.

• Funzione di rischio
  \(h(t\vert U)=h_0(t)\cdot U\)
  \(h(t\vert X, U)=h_0(t)\exp{(\beta 'X)}\cdot U\)
• Rischio marginale
  \(\mathbb{E}_U\{h(t\vert U)\}=h_0(t)\cdot \mathbb{E}_U\{U\}=h_0(t)\)
• Funzione di sopravvivenza
  \(S(t\vert X,U)=\exp{\big\{-\int_0^t h(s\vert X,U)ds\big\}}=\exp{\left \{ -U \exp{(\beta'X)}H_0(t) \right \}}\)
• Sopravvivenza marginale
  \(S(t)=\mathbb{E}\left \{ S(t\vert U)\right \}=\mathbb{E}\left \{\exp{\left [ -U \exp{(\beta'X)}H_0(t) \right ]} \right \}=\mathbf{L}\left\{ \exp{(\beta'X)} H_0(t)\right\}\)
• Trasformata di Laplace
  \(\mathbf{L}=\int e^{-zu}\cdot f(u)du\)
• La varianza della frailty può avere un valore contenuto e influenzare significativamente sia le covariate (sia come significatività che il valore) che la forma del rischio

Distribuzione della Frailty

Gamma

• Caratteristiche
  • Facile da standardizzare
    per ottenere \(\mathbb{E}(U)=1\) si impone \(U\sim\Gamma(k=\lambda, \lambda)\) con \(\sigma^2=1/\lambda\)
  • La vera distribuzione della frailty tra i sopravviventi tende a Gamma per \(t\rightarrow \infty\)
• Laplace esplicita
  \(\mathbf{L}=\int e^{-zu} f(u)du=\big(1+\frac{z}{\gamma}\big)^{-k}\)
• Sopravvivenza marginale
  \(S(t)=1/\left [ 1+\sigma^2 H_0(t) \right ]^{1/\sigma^2}\)
• Rischio marginale
  \(h(t)=h_0(t)/\left [ 1+\sigma^2 H_0(t) \right ]\)

Log-normale

• Caratteristiche
  \(X\sim\mathcal{N}(m,s^2)\rightarrow U=e^X \sim \log{N}\left (e^{\left ( m+\frac{s^2}{2}\right )},e^{\left ( 2m+s^2 \right )}(e^{s^2}-1) \right )\)
  \(f(u)=\frac{1}{\sqrt{2\pi}su}\exp{\left ( - \frac{\log{(u)}^2}{2s^2} \right )}\)
  • Forte legame con modello lineare ad effetti casuali
  • Più semplice la generalizzazione al caso multivariato
• Laplace non-esplicita

Modello Gompertz

Il modello esponenziale è un caso specifico.
\(f(t)=\lambda e^{\phi t} e^{-\frac{\lambda}{\phi} \left [\exp{(\phi t)}-1 \right ]}\) con \(\lambda > 0\)
\(S(t)=e^{-\frac{\lambda}{\phi} \left [\exp{(\phi t)}-1 \right ]}\)
\(h(t)=\lambda e^{\phi t}\)
\(h(t_i\vert X_i)=e^{\phi t_i} e^{\beta_0 +X_i' \beta}\) con \(\lambda=e^{\beta_0}\)
\(H(t)=\frac{\lambda}{\phi} \left [e^{\phi t}-1 \right ]\)
Se \(\phi=0\) allora è esponenziale
Se \(\phi<0\) rischio decrescente con il tempo (non applicabile alla mortalità)

Modello Gomperz-Makeham

\(h(t)=\lambda e^{\phi t}+c\) con \(c\) componente indipendente dal tempo dominante con l’avanzare del tempo.
Il modello distribuzione descrive bene i tassi di mortalità (principalmente 30-80 anni), successivamente il tasso di mortalità cresce più lentamente (late-life mortality deceleration), portando il rischio ad essere costante (plateau).

Modello Gamma-Gompertz

La late-life mortality deceleration è come una selezione (all’aumentare del tempo, sopravvivono gli individui più resistenti), quindi si introducono modelli con frailty per limitarne l’effetto (Mixed Proportional Hazard Model).
\(h(t_i\vert X_i)=e^{\phi t_i} e^{\beta_0 +X_i' \beta}\cdot Z_i\) con frailty Gamma \(Z\)
quindi risulterà
\(h(t_i\vert X_i)=\frac{\exp{(\phi t_i)} \exp{(\beta_0 +X_i' \beta)}}{1+\sigma \frac{\exp{(\beta_0 +X_i' \beta)}}{\phi} \left [\exp{(\phi t)}-1 \right ]}\)
con \(\sigma\) varianza della distribuzione gamma. Il rischio marginale ha forma di logistica con asintoto (plateau) che dipende dai parametri \(\phi\) e \(\sigma^2\) (se \(\sigma^2=0\) si ritorna a Gompertz).
Quindi con la frailty si ottiene la decelerazione della crescita del rischio.
Con \(\sigma^2\) bassa comunque la frailty può essere molto utile, bisogna valutare se variano gli effetti delle covariate rispetto al modello senza frailty e il livello di bontà di adattamento.

Duplice interpretazione

• Modello parametrico con distribuzione Gamma-Gompertz: la distribuzione dei tassi di mortalità per età non ha una forma Gompertz ma Gamma-Gompertz, cioè non cresce esponenzialmente ma ad un certo tempo comincia a decellerare
• Modello Gompertz con frailty Gamma: per i singoli individui la distribuzione del tasso di mortalità ha una forma Gompertz (forma esponenziale), ma a livello di popolazione con fragilità diverse all’interno, si crea una selezione e a livello di popolazione si osserva la decelerazione del rischio.

Modelli Frailty Univariati

Modello parametrico

Per fare inferenza con i modelli di frailty

• Verosimiglianza condizionata alle frailty non si può massimizzare perché non si conosce la frailty
  \(L(\beta,\theta \vert U_1,...,U_n)=\prod_{i=1}^n h(t_i \vert \beta, \theta, U_i)^{\delta _i} S(t_i \vert \beta, \theta, U_i)\) con \(\delta _i=0\) se la durata \(t_i\) è censurata, \(\theta\) parametri relativi alla forma del rischio (es. nel caso dell’esponenziale \(\theta\) è costante il valore di base del rischio), \(\theta\) parametro delle covariate
• Verosimiglianza marginale come valore atteso della condizionata (è una pseudo verosimiglianza, utile per ottenere le stime MV, ‘liberandosi’ dell’influenza della frailty)
  \(L(\beta,\theta,s^2)=\int L(\beta,\theta \vert U_1,...,U_n) d\Phi(U_i)\) con \(\Phi(U_i)\) distribuzione scelta delle frailty
• Integrazione della verosimiglianza marginale
  • Trasformazione di Laplace non-esplicita: integrazione numerica (approssimazione di Laplace, quadratura Gaussiana)
  • Trasformazione di Laplace esplicita: non richiede integrazione perché si ha forma esplicita

Esempio su R

Con le librerie survival e parfm.

## Speed-time tra modelli parametrici con frailty e 
# laplace esplicita (gamma) e non-esplicita (log-normale)
## SAS usa sempre e solo la procedura iterativa non
# utilizzando i vantaggi analitici della Laplace

# libs
library(survival)
library(parfm) # parametric frailty models

# df
data(kidney)
kidney$sex <- kidney$sex - 1

# modello parametrico Weibull con frailty distribuzione gamma
system.time(
    parfm(Surv(time,status)~sex+age+as.factor(disease), 
          cluster="id", data=kidney, 
          dist="weibull", frailty="gamma"))

   user  system elapsed 
  4.606   0.001   4.639 

# modello parametrico Weibull con frailty distribuzione log-normale
system.time(
    parfm(Surv(time,status)~sex+age+as.factor(disease), 
          cluster="id", data=kidney, 
          dist="weibull", frailty="lognormal", 
          method="Nelder-Mead", maxit=2000))

   user  system elapsed 
 11.775   0.000  11.784 

# modello parametrico Weibull con frailty distribuzione normale inversa
system.time(
    parfm(Surv(time,status)~sex+age, 
          cluster="id", data=kidney, 
          dist="weibull", frailty="ingau"))

   user  system elapsed 
  2.060   0.000   2.062 

# modello parametrico Weibull con frailty positive stable
system.time(
    parfm(Surv(time,status)~sex+age, 
          cluster="id", data=kidney, 
          dist="weibull", frailty="possta", 
          method="Nelder-Mead"))

   user  system elapsed 
  3.229   0.000   3.231 

Modello semi parametrico

I parametri disturbo non so solo le frailty ma anche il rischio di base.

Fattorizzazione della verosimiglianza:
\(L(\beta,\sigma^2,U)=\prod_{i=1}^n f(t_i , \delta_i, U_i \vert h_0(\cdot), \beta,\sigma^2)=L_1 (h_0(\cdot ),\beta)\cdot L_2(\sigma^2)\)

Failty note

Se le \(U_i\) fossero note, in \(L_1\) si sostituisce \(U_i=e^{\log{(U_i)}}\) e si stima usando il metodo della verosimiglianza parziale di Cox (le frailty diventano un offset, valore noto come l’ampiezza di osservazione degli eventi di una distribuzione di Poisson).
\(L_2\) con frailty note, sarebbe la verosimiglianza della distribuzione della frailty.

Frailty non-note

Due alternative per ottenere le stime

1. Algoritmo EM (Expectation-Maximization) con la verosimiglianza parziale, considerando come se le frailty fossero i dati mancanti (cfr EM, si ipotizzano valori casuali delle frailty si stimano le verosimiglianze parziali, si calcolano i valori attesi e si ripete fino a convergenza).
   • Frailty Gamma
   • Il rischio cumulato di base si stima con Nelson-Aalen (equivalente alla stima KM)
   • Valore atteso di \(\log{U}\) con distribuzione log-Gamma è noto
2. Verosimiglianza parziale penalizzata (utile per restringere una verosimiglianza piatta, pesando maggiormente alcuni valori del dominio del parametro da stimare)
   \(h(t\vert X,U)=h_0(t)e^{\beta ' X + W}\) con \(W=\log{U}\) se \(U\sim\log{\mathcal{N}}\rightarrow W\sim\mathcal{N}\)
   • Frailty log-normale
   • Frailty Gamma (stessi risultati di EM)

Shared Frailty Models

Applicazione dei modelli multilevel in contesto di dati di durata, con gli individui (unità di primo livello) all’interno di gruppi (unità di secondo livello).

Modelli univariati:

• Assegnano ad ogni individuo un livello di “fragilità”
• Mirano a tenere sotto controllo l’eterogeneità non osservata

Modelli Shared:

• Assegnano un livello di fragilità comune a un gruppo di unità statistiche
• Mirano a tenere sotto controllo la correlazione intraclasse, cioè la correlazione tra gli individui che appartengono agli stessi gruppi

Funzioni

• Funzione di rischio
  \(h(t_{ij}\vert X_{ij}, U_i)=h_0(t_{ij}) U_i e^{\beta ' X_{ij}}\) con \(i\) gruppo e \(j\) unità dentro il gruppo
• Sopravvivenza congiunta
  \(S(t_{i1,...,t_{in_i}}\vert X_{ij}, U_i)=\prod_{j=1}^{n_i} S(\cdot)=\exp{\left ( -U_i \sum_{j=1}^{n_i} H_0 (t_{ij}) e^{\beta' X_{ij}} \right ) }\)
• Sopravvivenza marginale per le unità appartenenti al $i-$esimo gruppo
  \(S(t_{i1,...,t_{in_i}}\vert X_{ij})=\mathbf{L} \left \{ \sum_{j=1}^{n_i} H_0 (t_{ij}) e^{\beta' X_{ij}} \right \}\), bisognerà tanti integrali quanti gruppi, non più quanti gli individui quindi è più veloce
• Inferenza analoga ai modelli univariati

Modelli Frailty a tempi Discreti

Problema dei ties. Nel modello di Cox ad esempio si creano problemi.
Si può stimare un modello a tempi discreti da un modello logistico a intercetta casuale.
Si hanno \(J\) intervalli e la probabilità di subire l’evento all’intervallo \(j-\)esimo è
\(P(t_{i-1}<T\le t_i)=F(t_i)-F(t_{i-1})=S(t_{i-1})-S(t_i)=f(t_i)=S(t_{i-1})\cdot h(t_i)\)
\(h(t_i)=P(t_{i-1}<T\le t_i\vert T\ge t_{i-1})=1-\frac{S(t_1)}{S(t_{i-1})}\)
la funzione di rischio nel discreto è una probabilità (condizionata) e varia tra 0 e 1.
\(S(t_{j})=\left[1-\left(S(t_{0})-\frac{S(t_{1})}{S(t_{0})}\right)\right]\cdot \left[1-\left(\frac{S(t_{1})-S(t_{2})}{S(t_{1})}\right)\right]\cdots \left[1-\left(\frac{S(t_{j-1})-S(t_{j})}{S(t_{j-1})}\right)\right]=\prod_{i=1}^j\left(1-h(t_i)\right)\)
La funzione di densità è la probabilità di subire l’evento all’intervallo \(j-\)esimo.
Si riesce a formulare tutto in funzione del rischio.

Modello a odds proporzionali

\[\log{\left(\frac{h(t_i;X)}{1-h(t_i;X)}\right)}=\log{\left(\frac{h(t_i)}{1-h(t_i)}\right)}+\beta' X\]

La funzione di rischio ora è una probabilità, quindi l’odds è una quantità sensata, non lo era in ambito continuo (poteva essere anche negativo).
Ricavata la funzione di verosimiglianza (costruita come contributi individuali divisi per censurati e non), si dimostra che è analoga alla verosimiglianza di un modello logistico (di una variabile \(y_{ik}\) relativa non solo all’individuo ma anche all’intervallo).

\[\log{\left(\frac{P(y_i=1)}{1-P(y_i=1)}\right)}=\beta_0+ \beta' X\]

Quindi per stimare il modello a odds proporzionali:

1. Si riorganizzano i dati nel formato ‘person-period’ (se era in formato ‘person data’), con un record per ogni intervallo di tempo
2. Si creano le variabili tempo-dipendenti
3. Si stima il modello con una regressione logistica, i cui coefficienti sono i medesimi del modello a odds proporzionali

Frailty univariato

Si inserisce un’intercetta casuale al corrispondente modello logistico.

Per stimare un modello frailty univariato si fa ricorso ad un modello logistico gerarchico (ad intercetta casuale): l’effetto casuale è condiviso dagli intervalli di tempo dello stesso individuo. Log della frailty fissa nel tempo ma è diversa per ogni individuo.

\[\log{\left(\frac{P(y_{ik}=1)}{1-P(y_{ik}=1)}\right)}=\beta_0+ \beta' X_{ik}+\alpha_i\]

Modello logistico gerarchico con unità di secondo livello l’individuo e di primo è l’intervallo. È un modello frailty univariato, non è Frailty Shared, perché la frailty è specifica per ogni individuo.
Se ci fosse un raggruppamento, si utilizzerebbe un modello logistico gerarchico con unità di terzo livello, sarebbe un modello Frailty Shared, perché la frailty fa riferimento al gruppo a cui appartiene l’individuo.

La distribuzione della log frailty tipicamente si sceglie normale (quindi frailty log normale) rispetto all’odds. Rispetto al rischio è la trasformata logit di una normale, quindi non è una distribuzione nota.

Modelli Multilivello o Gerarchici

Modelli Multilivello

Dati raggruppati in modo tale da ipotizzare più intercette e/o pendenze differenti

• Modelli ad intercetta variabile (\(n\) rette parallele)
• Modelli a pendenza variabile (effetti random)
• Modelli a intercetta e pendenza variabili

Il modello Multilevel come pooling parziale dei dati.

Modelli Gerarchici

La gerarchia si può intendere in due modi

1. Gerarchia Bayesiana, dove i dati si distribuiscono secondo una famiglia di parametro \(\theta_1\) e a sua volta il \(\theta_1\) si assume sia la realizzazione di una variabile casuale la cui distribuzione (a-priori) appartiene ad una famiglia di parametro \(\theta_2\) (si può continuare con \(\theta_3\), con distribuzione iper-a-priori, etc.)
2. Struttura gerarchica dei dati, quando unità statistiche di secondo stadio (I livello) appartengono a delle unità di primo stadio (II livello). Es.: pazienti (I livello) e ospedali (II livello), oppure nei dati longitudinali, individuo (II livello) e tempo (I livello).

Pooling

Quando si sintetizza l’informazione (es. media) schiacciando il livello superiore, ignorando la variabilità tra i gruppi, interna al livello. Al contrario, considerare tutti i gruppi appartenenti al livello superiore (no-pooling) porta sovrastimare la variabilità tra i gruppi del livello. Concetto analogo al trade-off distorsione-varianza.

Analisi multilevel senza covariate

Coefficiente di correlazione intraclasse

La costruzione che segue è specifica per i modelli lineari classici (e non GLM).

ANOVA ad una via con effetti casuali

Dato il modello con intercetta casuale e senza variabili indipendenti
Sia \(i\) unità di I livello e \(j\) di II livello
\(y_{ij}=\beta_{0j}+\epsilon_{ij}\) con \(\epsilon_{ij}\sim\mathcal{N}\left(0,\sigma^2_\epsilon\right)\)
Ipotizzando che \(\beta_{0j}=\gamma_{00}+U_{0j}\) con \(U_{0j}\sim\mathcal{N}\left(0,\sigma^2_{U_0}\right)\)
(\(\rightarrow\beta_{0j}\sim\mathcal{N}\left(\gamma_{00},\sigma^2_\epsilon\right)\)
e \(U_{0j}\perp \epsilon_{ij}\) sono mutuamente indipendenti (non vale sempre, ma i modelli ad effetti fissi non hanno \(U_{0j}\) quindi non richiedono questa assunzione).
La varianza dell’effetto casuale \(U_{0j}\) è la covarianza tra individui
appartenenti allo stesso gruppo
\(cov(y_{ij},y_{i'j})=E(y_{ij}y_{i'j})-E(y_{ij})E(y_{i'j})=var(U_{0j})=\sigma^2_{U_0}\)
La covarianza tra individui appartenenti allo stesso gruppo è la varianza dell’effetto casuale.
Si decide di fare il pooling (non serve modello multilevel) se la correlazione intraclasse è nulla (non è significativamente diversa da 0).

Coefficiente di correlazione traclasse:
\(\rho^{IC} (y_{ij},y_{i'j})=\frac{\sigma^2_{U_0}}{\sigma^2_{U_0}+\sigma^2_{\epsilon}}\) con \(\rho\in [0,1]\)
Se è presente correlazione viene meno la condizione iid per fare inferenza classica. Si genera una distorsione della varianza dei parametri (e non dei parametri). Però con stime robuste (sandwitch) si potrebbe ottenere comunque una stima corretta della varianza.

Varianza between-group

Esprime la variabilità tra le unità di II livello.
Con gruppi omogenei:
\(\sigma^2_{\small{\mbox{between}}}=\frac{1}{N-1}\sum_{j=1}^N (\bar{y}._{j}-\bar{y}..)^2\)
Il valore atteso è dato dal suo vero valore più la varianza introdotta dall’errore di campionamento:
\(E\big(\sigma^2_{\small{\mbox{between}}}\big)=\sigma^2_{U_0}+\frac{\sigma^2_\epsilon}{\hat{n}}\)
\(\hat{n}=\frac{1}{N-1}\left \{ M - \frac{\sum_j n_j^2}{M} \right \}=\bar{n}-\frac{s^2(n_j)}{N\bar{n}}=\) dimensione media delle unità di II livello,
con \(M\) numerosità unità I livello, \(N\) numerosità II livello,
\(\bar{n}=M/N\) e \(s^2(n_j)=\frac{1}{N-1}\sum_{j=1}^N (n_j - \bar{n})^2\)

Con gruppi non omogenei:
\(\sigma^2_{\small{\mbox{between}}}=\frac{1}{\hat{n}(N-1)}\sum_{j=1}^N n_j(\bar{y}._{j}-\bar{y}..)^2\)

Varianza within-group

È una media pesata delle varianze all’interno delle unità di II livello.
\(\sigma^2_{\small{\mbox{within}}}=\frac{1}{M-N}\sum_{j=1}^N \sum_{i=1}^{n_j}(y_{ij}-\bar{y}._j)^2\)
\(\sigma^2_{\small{\mbox{total}}}=\frac{1}{M-1}\sum_{j=1}^N \sum_{i=1}^{n_j}(y_{ij}-\bar{y}..)^2=\frac{M-N}{M-1}\sigma^2_{\small{\mbox{within}}}+\frac{\hat{n}(N-1)}{M-1}\sigma^2_{\small{\mbox{between}}}\)

Coefficiente di correlazione con varianza between e within

In un modello senza predittori, si ha
\(\hat{\sigma}^2_\epsilon=\sigma^2_{\small{\mbox{within}}}\)
\(\hat{\sigma}^2_{U_0}=\sigma^2_{\small{\mbox{between}}}+\frac{\sigma^2_\epsilon}{\hat{n}}\)
Potrebbe accadere che stimando un modello senza predittori, si ottenga un coeff. elevato che suggerisca l’utilizzo di un effetto casuale specifico per i gruppi, ma inserendo qualche predittore il coeff. potrebbe diminuire e quindi l’intercetta casuale potrebbe non essere più necessaria.

Analisi multilevel con covariate

\(y_{ij}=\alpha+\beta x_{ij}+\epsilon_{ij}\)
con eterogeneità non osservata, il vero modello è
\(y_{ij}=\gamma_i+\beta x_{ij}+\epsilon_{ij}\) con \(\gamma_i\) eterogeneità non osservata.

Rimozione eterogeneità non osservata

Con alcune trasformazioni, si può costruire un modello ad effetti fissi, che non ha il problema dell’assunzione \(U_{0j}\bot \epsilon_{ij}\) e garantisce una stima di \(\beta\) non distorta, ma non posso stimare \(\alpha\) né \(\gamma_i\).

Trasformata within-group

\(y_{it}-\bar{y_i}\)
Elimino la variabilità between, stimando \(\beta\) solo con la variabilità within.
Utile per avere solo una stima non distorta di \(\beta\), ma usando unicamente la variabilità within.
Nei dati panel è più la variabilità tra individui (between) che la variabilità dello stesso individuo in anni diversi (within), quindi si perde informazione.

Trasformata first difference

\(y_{it}-y_{it-1}\)

Modellazione eterogeneità non osservata

Modello pooling (underfitting)

Modello con intercetta fissa: stima un’intercetta uguale per tutti
\(y_{ij}=\beta_0+\beta_1 X_{ij}+\epsilon_{ij}\)

Modello no-pooling (overfitting)

Modello con intercetta specifica per ogni gruppo: per stimare l’intercetta di un gruppo usa i dati solo di quel gruppo
\(y_{ij}=\beta_{0j}+\beta_1 X_{ij}+\epsilon_{ij}\) con \(\beta_{0j}\) fissa

Modello gerarchico o di pooling parziale

Modello con intercetta casuale, specifica per ogni gruppo.
\(y_{ij}=\beta_{0j}+\beta_1 X_{ij}+\epsilon_{ij}\) con \(\beta_{0j}\sim\mathcal{N}(\gamma_{00},\sigma^2_{\beta})\) e
\(\gamma_{00}\) intercetta globale, la media delle intercette

Il modello tenderà ad un modello pooling se

• \(\sigma^2_{\beta}\rightarrow 0\), l’intercetta casuale ha varianza \(0\), quindi si ha una sola intercetta e di conseguenza \(\gamma_{00}=\beta_0\)
• La numerosità campionaria è ridotta (seguo più il modello)

Il modello tenderà ad un modello no-pooling se

• \(\sigma^2_{\beta}\rightarrow \infty\) modello no-pooling, in quanto una normale con varianza infinita è piatta e
  in ottica bayesiana è come se fosse una priori non informativa quindi si utilizzano tutti i gruppi
• La numerosità campionaria è elevata (seguo più i dati)

Modelli ad effetti casuali o ad effetti misti

Modellazione con pendenza casuale
\(y_{ij}=\beta_{0j}+\beta_{1j}X_{ij}+\epsilon_{ij}\) con \(\begin{pmatrix} \beta_{0j} \\ \beta_{1j} \end{pmatrix}\sim\mathcal{N}\left(\begin{pmatrix} \gamma_{00} \\ \gamma_{10} \end{pmatrix}, \begin{pmatrix} \sigma^2_{\beta_0} & \rho\sigma_{\beta_0}\sigma_{\beta_1} \\ \rho\sigma^2_{\beta_1} & \sigma_{\beta_0}\sigma_{\beta_1} \end{pmatrix}\right)\)

Modelli non nidificati

I gruppi presi non sono conteninuti l’uno nell’altro.

Modello nidificato

Dato l’individuo \(i\) (unità di I livello), appartenente alla famiglia \(j\) (unità di II livello) e al gruppo \(k\) (unità di III livello)
\(y_{ijk}=\alpha_k+\gamma_{jk}+\beta x_{ijk}+\epsilon_{ijk}\) con \(\alpha_k\sim\mathcal{N}(\alpha_0,\sigma^2_\alpha)\)

Modello non-nidificato

Dato l’individuo \(i\) (unità di I livello), appartenente alla classe d’età \(j\) (unità di II livello) e alla nazione \(k\) (unità di II livello)
\(y_{i(j,k)}=\alpha_k+\gamma_{j}+\beta x_{ijk}+\epsilon_{ijk}\) con \(\gamma_j\sim\mathcal{N}(\gamma_0,\sigma^2_\gamma)\)

Stima Bayesiana empirica

Stima dell’intercetta casuale. Non è una stima perché non è un parametro ma una variabile casuale, il termine giusto sarebbe previsione del valore.
Prevede il valore di \(\beta_{0j}\) per un gruppo \(j\), si prova che la previsione è un valore atteso.
Stima bayesiana empirica del modello ad intercetta casuale senza predittori.
Stima bayesiana empirica di \(\hat{\beta_{0j}}\) (modello ad intercetta casuale senza predittori) di Snijder & Boskers (analoga a Gelman & Hill): media pesata della media specifica del gruppo \(j\) (no-pooling) e della media totale (pooling)

\[\hat{\beta}_{0j}=\frac{\sigma^2_{\beta_0}\bar{y}._j +\frac{\sigma^2_\epsilon}{n_j}\bar{y}..}{\sigma^2_{\beta_0}+\sigma^2_{\epsilon}/n_j}\]

Teoria Bayesiana

Elicitazione: rappresentazione della conoscenza a priori in una distribuzione (a priori).

Dati
\(y_i\sim\mathcal{N}(\mu,\sigma^2_0)\) con \(\sigma^2_0\) noto e \(\mu\) ignoto
\(\mu\sim\mathcal{N}(\mu_0,\tau^2_0)\) con \(\mu_0\) e \(\tau^2_0\) iperparametri della distribuzione a priori

Si dimostra che la “stima’’ Bayesiana empirica è analoga alla media a posteriori \(E(\mu\vert y)\)

Tramite il teorema di Bayes (e algoritmi iterativi quali Metropolis-Hastings, Gibbs sampling o Hamiltonian Monte Carlo per risolvere l’integrale, o si usano le distribuzioni coniugate come questo caso) la distribuzione a posteriori:

\[f(\mu\vert y)=\frac{f(y\vert \mu)\cdot f(\mu)}{\int_\mu f(y\vert \mu)\cdot f(\mu)d\mu}\]

si dimostra che la distribuzione a posteriori è la seguente

\[\mu\vert y\sim\mathcal{N}\left (\frac{\tau^2_0\bar{y}+\frac{\sigma^2_0}{n}\mu_0}{\tau^2_0+\frac{\sigma^2_0}{n}},\frac{\sigma^2_0\tau^2_0}{\sigma^2_0+n\tau^2_0}\right )\]

Il modello gerarchico è un compromesso tra il modello pooling e no-pooling, la stima Bayesiana empirica è un compromesso tra la media totale e la media specifica del gruppo \(j\).
Il modello multilevel effettua un ‘borrowing’ dell’informazione prendendo anche da altri gruppi.
La stima bayesiana è una media pesata della media campionaria (che in un modello normale di media ignota e varianza ignota è la stima MV, quindi usando solo i dati) e la media a priori.

• \(n\rightarrow\infty\) la media a posteriori tende alla stima MV
• \(\tau^2_0\rightarrow\infty\) meno è informativa la priori, più peso ha alla stima MV e meno la priori
• \(\sigma^2_0\rightarrow\infty\) la varianza dei dati, che è nota, se è alta più importanza avrà la media a priori

Il valore atteso della distribuzione a posteriori, differisce dalla Bayesiana empirica, in quanto in quest’ultima non si assume una distribuzione a priori e al posto della media e varianza a priori si hanno le stime (MV) del modello pooling.

La verosimiglianza penalizzata, può essere vista come una variante frequentista della distribuzione a priori.

Modelli lineari generalizzati gerarchici

Generalized Linear Mixed Models (GLMM), analogia LM\(\rightarrow\)GLM.
Per la previsione del tasso di successo, si effettua una media pesata di ogni gruppo

\[\theta_j=\frac{\sum_{l\in j} N_l \theta_l}{\sum_{l\in j} N_j}\]

Questo però nel caso di più variabili discrete a diversi livelli, il campione necessario deve essere enorme per soddisfare tutte le combinazioni. Per evitare di riempire tutte le informazioni, si possono usare i modelli gerarchici per fare ‘borrowing’ dell’informazione laddove è presente (rischio: shrinkage to mean).

Modello a gerarchie imperfette: alcune gerarchiche sono dello stesso livello.

GLMM Logit

\(\mbox{Logit}\big\{Pr(y_{ij(k,l)}=1)\big\}\)

GLMM Poisson

Posso farlo sul tasso invece che sul semplice numero, ad esempio il tasso di migratorietà, con intercetta casuale sulle nazioni.

Un altro caso: tasso di mortalità prematura. Si possono ipotizzare distribuzioni differenti modellando la mistura. Oppure con un modello gerarchico, si tiene fissa la mortalità adulti e variabile la mortalità prematura (come variabile effetto casuale).

GLMM Multinomiale

• Modello a destinazioni multiple
• Rischi competitivi (non sono indipendenti tra loro gli eventi)
• Estensione del Logit
• Problema dell’indipendenza da alternative irrilevanti

Stima dei parametri

I parametri con OLS sono Best Linear Unbiased Estimator (BLUE) se vale l’omoschedasticità.

Con un modello gerarchico, se si vuole fare una stima basata sulla MV, l’inferenza sarebbe legata a meno due volte la log-verosimiglianza.
Il problema è che bisogna conoscere la matrice delle varianze degli effetti casuali, che è sconosciuta e si otterrebbero stime distorte (perché non si tiene conto della perdita dei g.d.l. per le stime degli altri parametri).

Il modello lineare si può stimare con REML (stime non distorte di \(\sigma^2\), non consente test TRV) o ML (stime distorte di \(\sigma^2\) ma consente test TRV).
Il modello logistico lo si stima con la verosimiglianza marginale.

L’intercetta casuale e/o effetti casuali si stimano con la stima bayesiana empirica.

Restricted (o Residual) Maximum Likelihood

La REML, si basa su una combinazione lineare dei dati affinché la distribuzione non dipenda da \(\beta\), si stimano i parametri che definiscono la matrice di varianze e covarianze con il metodo MV, e dopo si procede ad una stima anche dei parametri \(\beta\).

La stima non distorta della varianza di una v.a. \(Y\sim\mathcal{N}(\mu,\sigma^2)\) è una stima REML. Si ha una funzione di verosimiglianza, con \(\mu\) e \(\sigma^2\) e stima di \(\sigma^2\) dipende dalla stima di \(\mu\), quindi nella stima MV non tengo conto che perdo un grado di libertà per stimare \(\mu\) e poi costruire all’interno la stima di \(\sigma^2\).

Proprietà

• Le stime REML restituiscono stime della varianza non distorta, diversamente dalla MV
• La stime REML sono analoghe al metodo dei Minimi Quadrati Pesati.
• La verosimiglianza ‘ristretta’, ottenuta dalla REML non gode delle stesse proprietà della stima MV ordinaria, e il test rapporto di verosimiglianze (TRV) non è possibile

Come scegliere tra REML e MV

Dipende da \(n\) e \(p\) se

• \(n\) grande e \(p\) piccolo, la distorsione tra le varianze è piccola
• \(n\) è piccolo e \(p\) grande, ci può essere differenza tra le due stime

Utili

Century Months

Data in C.M. : numero di mesi da inizio secolo 01/01/1900

\(\mbox{C.M.}=\mbox{YY}\times 12+\mbox{MM}\)
es. Marzo 1946: \(\mbox{C.M.}=46\cdot 12+3=555\)

\(\mbox{YY}=(\mbox{C.M.}-1)/12+1900\)
\(\mbox{MM}=\mbox{C.M.}-(\mbox{intero(YY)}\times 12)\)
es. \(555 \rightarrow \mbox{Anno}=(555-1)/12=46.16,\quad \mbox{Mese}=555-(46\cdot 12)=555-552=3\)

Risorse

• Andrew Gelman
• Codice R su RADON per modelli multilevel
• Mixed effects modeling

…