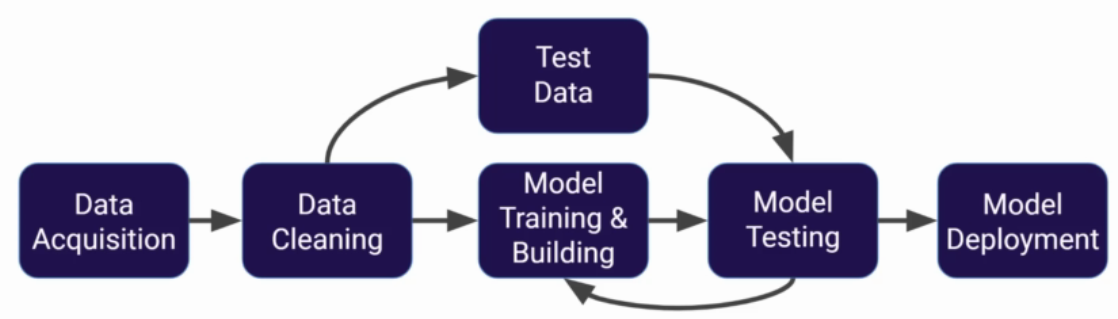
Machine Learning Process
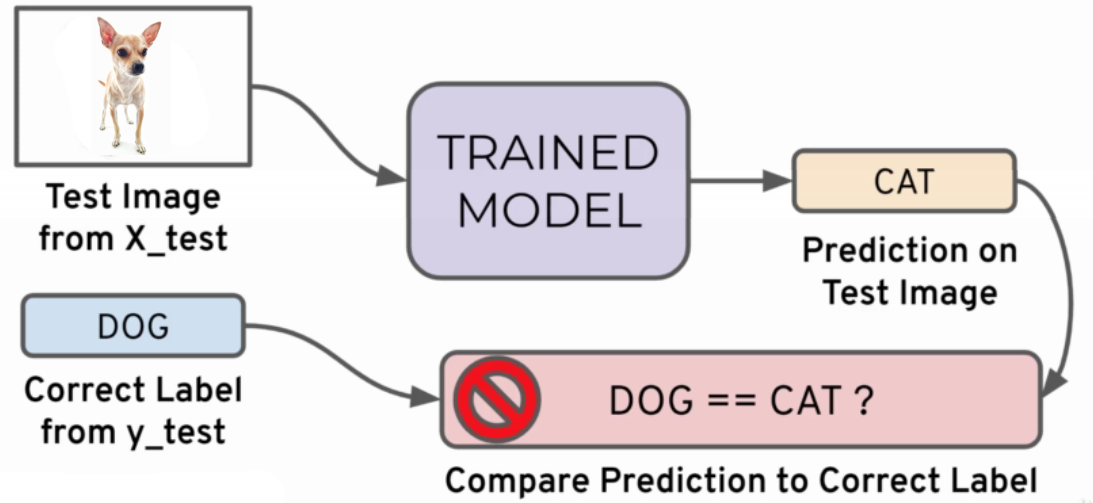
Binary Classification
HTML Table Generator
Latex Editor
Confusion Matrix
|
|
Predicted Class |
|
|
|
1 |
0 |
|
| Actual Class |
1 |
TP |
FN |
(P) |
| 0 |
FP |
TN |
(N) |
\[T = True \\ F = False \\ P = Positive \\ N = Negative\]
\[\alpha = False Positive Rate = \frac{FP}{FP+TN}\]
\[\beta = False Negative Rate = \frac{FN}{TP+FN}\]
\[Accuracy = \frac{TP+TN}{TP+TN+FP+FN} = \frac{TP+TN}{P+N}\]
\[Precision = Positive Predictive Value = \frac{TP}{TP+FP}\]
\[Recall = Sensitivity = True Positive Rate = \frac{TP}{TP+FN} = \frac{TP}{P}\]
\[F_{1}Score = 2 \cdot \frac{Precision \cdot Recall}{Precision + Recall} = \frac{2 \cdot TP}{2 \cdot TP+FP+FN}\]
Bonus meme

Evaluation
Evaluating Regression
MAE = Mean Absolute Error = \(\frac{1}{n} \sum_{i=1}^{n} \left | y_{i}-\widehat{y}_i \right |\)
Poco sensibile agli outliers però rappresenta l’errore medio
MSE = Mean Squared Error = \(\frac{1}{n} \sum_{i=1}^{n} \left ( y_{i}-\widehat{y}_i \right )^2\)
Unità di misura al quadrato
RMSE = Root Mean Square Error = \(\sqrt(\frac{1}{n} \sum_{i=1}^{n} \left ( y_{i}-\widehat{y}_i \right )^2)\)
Risolve i problemi precedenti
Se rapportati alla media del fenomeno si ha un’idea migliore di quanto è impattante l’errore rispetto la scala di misura
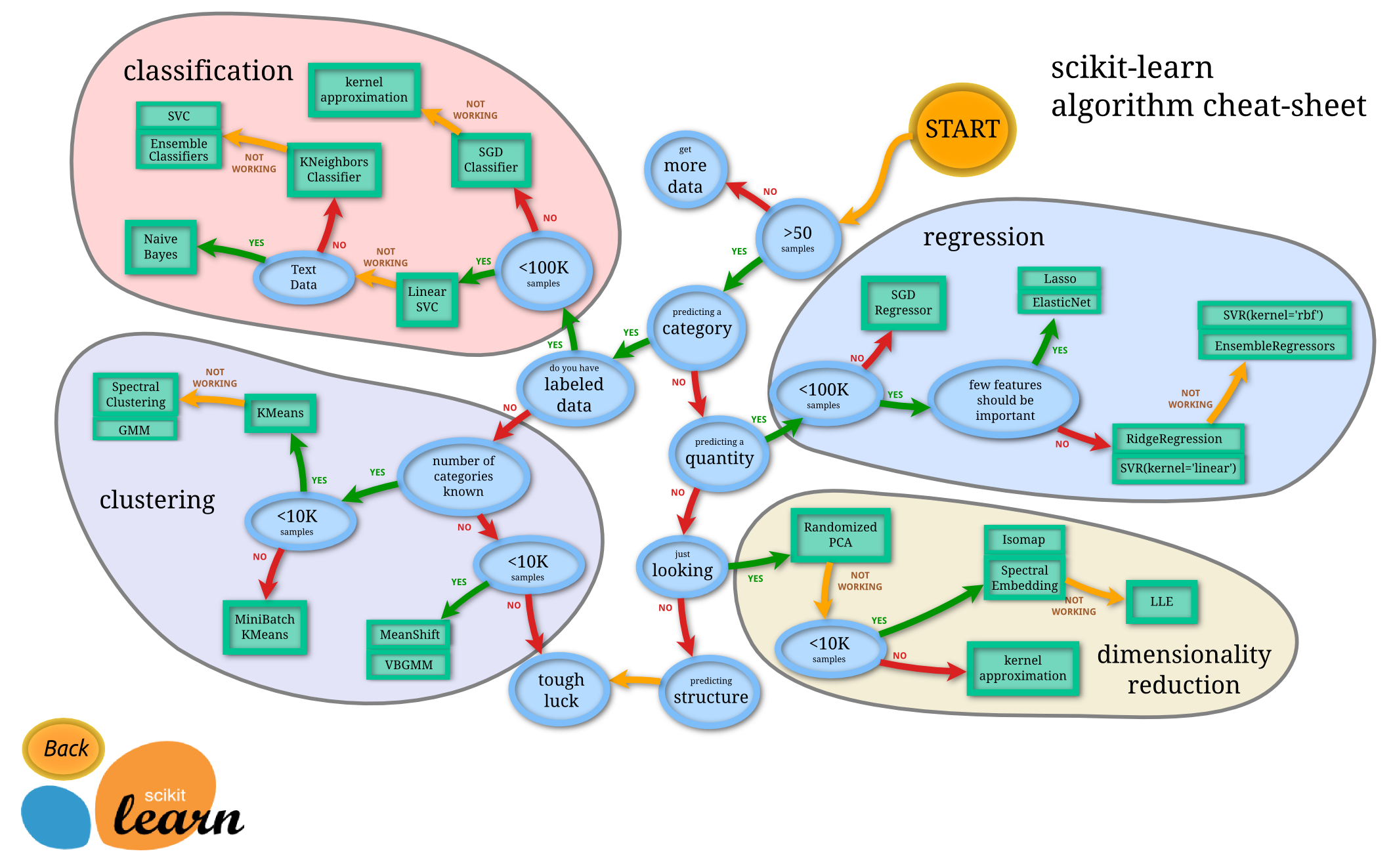
Choosing an Algorithm
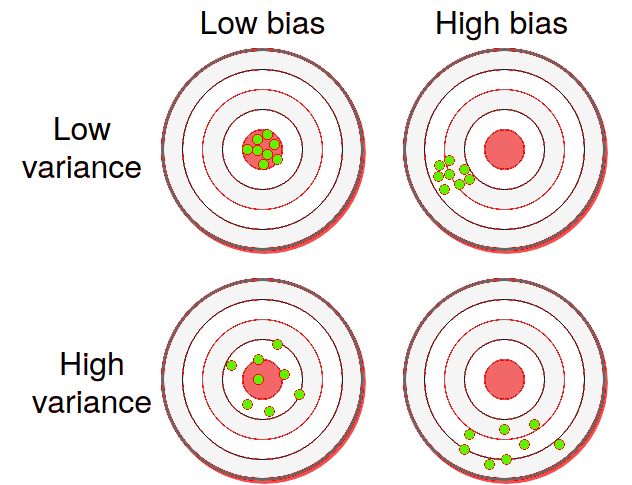
Bias-Variance Trade-Off
\[MSE\left (\hat{\theta}\right ) \\
= \mathbb{E}\left [\left (\hat{\theta}-\theta \right)^2\right ] \\
= \mathbb{E}\left [\left (\hat{\theta}-\mathbb{E}\left (\hat{\theta}\right )+\mathbb{E}\left (\hat{\theta}\right )+\theta \right)^2\right ] \\
= \ldots \\
= \mathbb{E}\left [\left (\hat{\theta}-\mathbb{E}\left (\hat{\theta}\right ) \right)^2\right ] + \mathbb{E}\left [\left (\mathbb{E}\left (\hat{\theta}\right )-\theta \right)^2\right ] \\
= Var(\hat{\theta})+Bias(\hat{\theta},\theta)^2\]
L’overfitting si genera riducendo il bias perché si introducono più parametri, ma la varianza della stima aumenta.





