Alberto

Alberto

Experience is not what
happens to a man;
it is what a man does
with what happens to him.
-Aldous Huxley

Python: Principal Component Analysis

Utilizzo l’environment conda py3

1

~$ conda activate py3

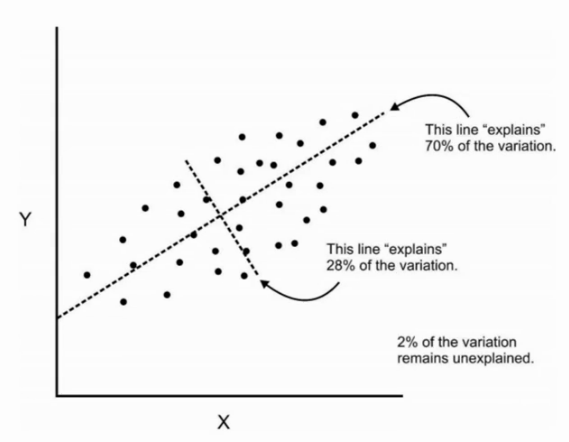
PCA

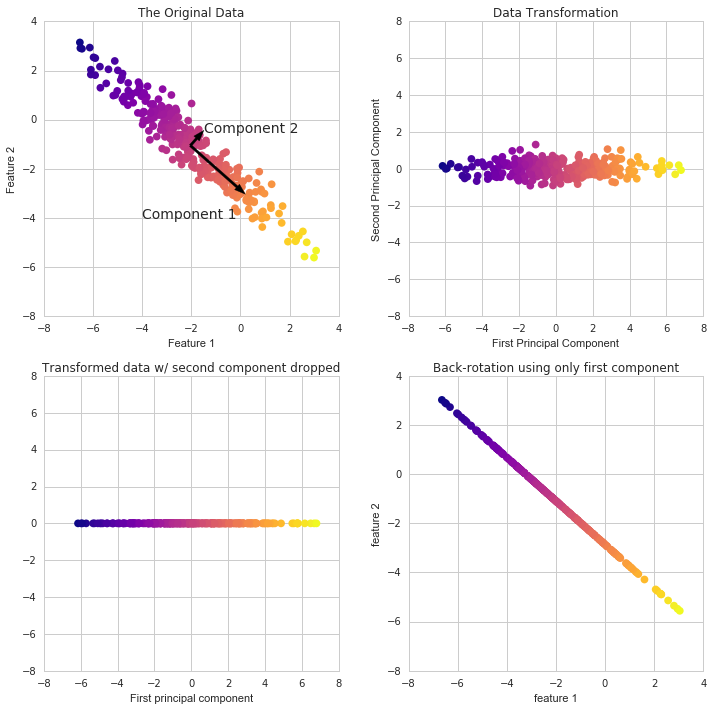
1
2
3
4
5
6
7
8
9
10

# lib
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
%matplotlib inline

from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

1
2
3

# cancer data
cancer = load_breast_cancer()
cancer.keys()

1

dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename'])

1
2
3

# df
df = pd.DataFrame(cancer['data'],columns=cancer['feature_names'])
df.head()
mean radius mean texture mean perimeter mean area mean smoothness mean compactness mean concavity mean concave points mean symmetry mean fractal dimension ... worst radius worst texture worst perimeter worst area worst smoothness worst compactness worst concavity worst concave points worst symmetry worst fractal dimension
0 17.99 10.38 122.80 1001.0 0.11840 0.27760 0.3001 0.14710 0.2419 0.07871 ... 25.38 17.33 184.60 2019.0 0.1622 0.6656 0.7119 0.2654 0.4601 0.11890
1 20.57 17.77 132.90 1326.0 0.08474 0.07864 0.0869 0.07017 0.1812 0.05667 ... 24.99 23.41 158.80 1956.0 0.1238 0.1866 0.2416 0.1860 0.2750 0.08902
2 19.69 21.25 130.00 1203.0 0.10960 0.15990 0.1974 0.12790 0.2069 0.05999 ... 23.57 25.53 152.50 1709.0 0.1444 0.4245 0.4504 0.2430 0.3613 0.08758
3 11.42 20.38 77.58 386.1 0.14250 0.28390 0.2414 0.10520 0.2597 0.09744 ... 14.91 26.50 98.87 567.7 0.2098 0.8663 0.6869 0.2575 0.6638 0.17300
4 20.29 14.34 135.10 1297.0 0.10030 0.13280 0.1980 0.10430 0.1809 0.05883 ... 22.54 16.67 152.20 1575.0 0.1374 0.2050 0.4000 0.1625 0.2364 0.07678

5 rows × 30 columns

1
2
3
4

# scaling data
scaler = StandardScaler()
scaler.fit(df)
scaled_data = scaler.transform(df)

1
2
3

# PCA
pca = PCA(n_components=2)
pca.fit(scaled_data)

1

PCA(n_components=2)

1
2

# trasform data to two components (da 30 colonne a 2)
x_pca = pca.transform(scaled_data)

1
2

print(scaled_data.shape)
print(x_pca.shape)

1
2

(569, 30)
(569, 2)

1
2
3
4
5

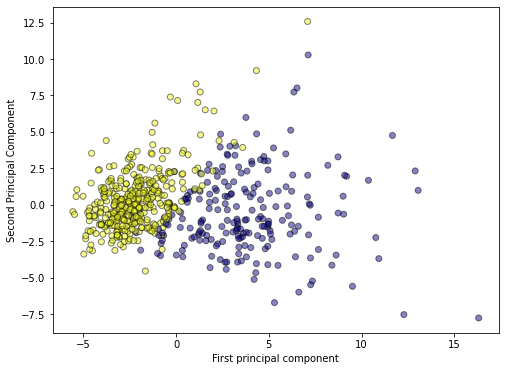
# plot PCA
plt.figure(figsize=(8,6))
plt.scatter(x_pca[:,0],x_pca[:,1],c=cancer['target'],cmap='plasma',edgecolors='black',alpha=0.5)
plt.xlabel('First principal component')
plt.ylabel('Second Principal Component')

1

Text(0, 0.5, 'Second Principal Component')

png

Coefficients

1
2
3
4

# interpretazioni coefficienti
# correlazione tra le variabili e le componenti
df_comp = pd.DataFrame(pca.components_,columns=cancer['feature_names'])
df_comp.head()
mean radius mean texture mean perimeter mean area mean smoothness mean compactness mean concavity mean concave points mean symmetry mean fractal dimension ... worst radius worst texture worst perimeter worst area worst smoothness worst compactness worst concavity worst concave points worst symmetry worst fractal dimension
0 0.218902 0.103725 0.227537 0.220995 0.142590 0.239285 0.258400 0.260854 0.138167 0.064363 ... 0.227997 0.104469 0.236640 0.224871 0.127953 0.210096 0.228768 0.250886 0.122905 0.131784
1 -0.233857 -0.059706 -0.215181 -0.231077 0.186113 0.151892 0.060165 -0.034768 0.190349 0.366575 ... -0.219866 -0.045467 -0.199878 -0.219352 0.172304 0.143593 0.097964 -0.008257 0.141883 0.275339

2 rows × 30 columns

1
2
3

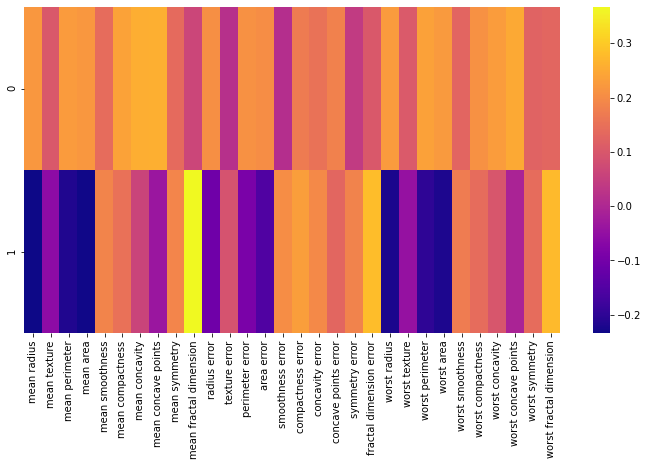
# heatmap
plt.figure(figsize=(12,6))
sns.heatmap(df_comp,cmap='plasma')

1

<matplotlib.axes._subplots.AxesSubplot at 0x7fee706d6d50>

png

Biplot

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

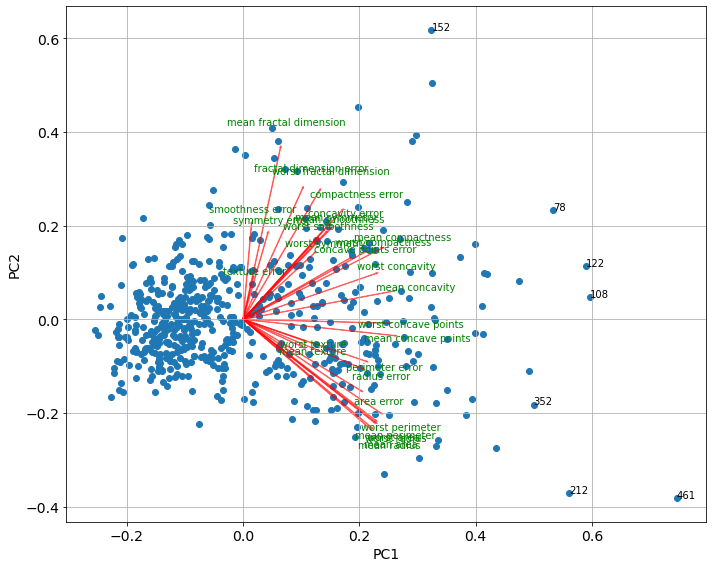
# il biplot è la rappresentazione grafica delle due prime componenti
# utile anche per identificare gli outliers

# funzione per il biplot
def biplot(score,coeff,y=None,labels=None):
    xs = score[:,0] # projection of PC1
    ys = score[:,1] # projection of PC2
    n = coeff.shape[0]
    scalex = 1.0/(xs.max() - xs.min())
    scaley = 1.0/(ys.max() - ys.min())
    plt.scatter(xs * scalex,ys * scaley, c = y)
    
    # aggiungo frecce
    for i in range(n):
        plt.arrow(0, 0, coeff[i,0], coeff[i,1],color = 'r',alpha = 0.5)
        if labels is None:
            plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, "Var"+str(i+1), color = 'g', ha = 'center', va = 'center')
        else:
            plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, labels[i], color = 'g', ha = 'center', va = 'center')

    # aggiungo flag outliers
    for i in range(len(xs)):
        if ((xs[i]>np.quantile(xs,0.99)) | (ys[i]>np.quantile(xs,0.99))):
            plt.text(xs[i] * scalex,ys[i] * scaley, str(i))

    # etichette
    plt.xlabel("PC{}".format(1), size=14)
    plt.ylabel("PC{}".format(2), size=14)
    plt.grid()
    plt.tick_params(axis='both', which='both', labelsize=14)
    plt.tight_layout()

1
2
3
4
5
6
7
8

# plot
plt.figure(figsize=(10,8))
biplot(score=x_pca,coeff=np.transpose(pca.components_),labels=df.columns)

# se ci fossero più componenti plotto solo le prime due (nb. sono array non dataframes)
# score=x_pca[:,0:2],coef=np.transpose(pca.components_[0:2, :])

# le variabili nella stessa direzione sono correlate

png

1
2

# esempio stessa direzione
np.corrcoef(df['worst perimeter'],df['mean perimeter'])[1,0]

1

0.9703868870426392

Outliers

1
2
3

# l'osservazione 461 è outliers per la prima componente, che ha coefficienti positivi verso le variabili 
# infatti i valori delle sue variabili sono vicini ai massimi (vedi il describe)
x_pca[461,]

1

array([16.31923323, -7.7758528 ])

1
2
3
4

# l'osservazione 152 è outliers per la seconda componente
# la PC2 ha coefficienti negativi verso le variabili tranne per 'mean fractal dimension'
# infatti i valori delle sue variabili sono vicini ai minimi, tranne per 'mean fractal dimension' che è elevata
x_pca[152,]

1

array([ 7.09330671, 12.57319423])

1
2

# describe stats assieme a due outliers
pd.concat([df.describe(),df.iloc[[461,152]]],axis=0)
mean radius mean texture mean perimeter mean area mean smoothness mean compactness mean concavity mean concave points mean symmetry mean fractal dimension ... worst radius worst texture worst perimeter worst area worst smoothness worst compactness worst concavity worst concave points worst symmetry worst fractal dimension
count 569.000000 569.000000 569.000000 569.000000 569.000000 569.000000 569.000000 569.000000 569.000000 569.000000 ... 569.000000 569.000000 569.000000 569.000000 569.000000 569.000000 569.000000 569.000000 569.000000 569.000000
mean 14.127292 19.289649 91.969033 654.889104 0.096360 0.104341 0.088799 0.048919 0.181162 0.062798 ... 16.269190 25.677223 107.261213 880.583128 0.132369 0.254265 0.272188 0.114606 0.290076 0.083946
std 3.524049 4.301036 24.298981 351.914129 0.014064 0.052813 0.079720 0.038803 0.027414 0.007060 ... 4.833242 6.146258 33.602542 569.356993 0.022832 0.157336 0.208624 0.065732 0.061867 0.018061
min 6.981000 9.710000 43.790000 143.500000 0.052630 0.019380 0.000000 0.000000 0.106000 0.049960 ... 7.930000 12.020000 50.410000 185.200000 0.071170 0.027290 0.000000 0.000000 0.156500 0.055040
25% 11.700000 16.170000 75.170000 420.300000 0.086370 0.064920 0.029560 0.020310 0.161900 0.057700 ... 13.010000 21.080000 84.110000 515.300000 0.116600 0.147200 0.114500 0.064930 0.250400 0.071460
50% 13.370000 18.840000 86.240000 551.100000 0.095870 0.092630 0.061540 0.033500 0.179200 0.061540 ... 14.970000 25.410000 97.660000 686.500000 0.131300 0.211900 0.226700 0.099930 0.282200 0.080040
75% 15.780000 21.800000 104.100000 782.700000 0.105300 0.130400 0.130700 0.074000 0.195700 0.066120 ... 18.790000 29.720000 125.400000 1084.000000 0.146000 0.339100 0.382900 0.161400 0.317900 0.092080
max 28.110000 39.280000 188.500000 2501.000000 0.163400 0.345400 0.426800 0.201200 0.304000 0.097440 ... 36.040000 49.540000 251.200000 4254.000000 0.222600 1.058000 1.252000 0.291000 0.663800 0.207500
461 27.420000 26.270000 186.900000 2501.000000 0.108400 0.198800 0.363500 0.168900 0.206100 0.056230 ... 36.040000 31.370000 251.200000 4254.000000 0.135700 0.425600 0.683300 0.262500 0.264100 0.074270
152 9.731000 15.340000 63.780000 300.200000 0.107200 0.159900 0.410800 0.078570 0.254800 0.092960 ... 11.020000 19.490000 71.040000 380.500000 0.129200 0.277200 0.821600 0.157100 0.310800 0.125900

10 rows × 30 columns

1
2

# pulisco il workspace
%reset -f

Tags: ,

Updated:

You may also enjoy